Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 12 trang 85 SGK Toán 8 tập 2 – Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và phù hợp với chương trình học Toán 8 hiện hành. Hãy cùng theo dõi để có kết quả học tập tốt nhất!
Bóng của một căn nhà trên mặt đất có độ dài 6 m
Đề bài
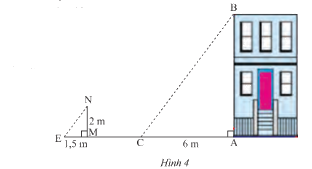
Bóng của một căn nhà trên mặt đất có độ dài 6 m. Cùng thời điểm đó, một cọc sắt cao 2 m cắm vuông góc với mặt đất có bóng dài 1,5m (Hình 4). Tính chiều cao của ngôi nhà.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Cùng một thời điểm thì góc của tia nắng tạo với mặt đất tại mọi vị trí là như nhau.
- Nếu tam giác vuông này có một góc nhọn bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = k\)
Lời giải chi tiết
Vì cùng một thời điểm thì góc tạo bởi tia nắng mặt trời và mặt đất là những góc bằng nhau. Do đó, \(\widehat {NEM} = \widehat {BCA}\).
Xét tam giác \(NEM\) và tam giác \(BCA\) có:
\(\widehat {NEM} = \widehat {BCA}\) (chứng minh trên)
\(\widehat {NME} = \widehat {BAC} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta NEM\backsim\Delta BCA\) (g.g)
Suy ra, \(\frac{{EM}}{{CA}} = \frac{{MN}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{1,5}}{6} = \frac{2}{{AB}} \Rightarrow AB = \frac{{2.6}}{{1,5}} = 8\).
Vậy chiều cao của ngôi nhà là 8m.
Bài 12 trang 85 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về tính chất của hình thang cân để giải quyết các bài toán liên quan đến việc chứng minh, tính toán độ dài cạnh, góc và đường trung bình của hình thang cân.
Bài 12 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập và đưa ra lời giải chi tiết.
Giả sử đề bài yêu cầu chứng minh tứ giác ABCD là hình thang cân. Để chứng minh điều này, chúng ta cần chứng minh hai cạnh đáy AB và CD song song, và hai cạnh bên AD và BC bằng nhau.
Bước 1: Chứng minh AB // CD
Sử dụng các kiến thức về góc so le trong, góc đồng vị hoặc tổng hai góc trong cùng phía bằng 180 độ để chứng minh hai đường thẳng AB và CD song song.
Bước 2: Chứng minh AD = BC
Sử dụng các trường hợp bằng nhau của tam giác (cạnh - cạnh - cạnh, cạnh - góc - cạnh, góc - cạnh - góc) để chứng minh hai tam giác có các cạnh tương ứng bằng nhau.
Sau khi chứng minh được tứ giác là hình thang cân, chúng ta có thể sử dụng các tính chất của hình thang cân để tính toán các yếu tố hình học của nó.
Ví dụ: Tính độ dài cạnh AD biết AB = 5cm, CD = 10cm và BC = 7cm.
Vì ABCD là hình thang cân nên AD = BC = 7cm.
Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên. Độ dài đường trung bình của hình thang bằng nửa tổng độ dài hai đáy.
Công thức: MN = (AB + CD) / 2 (với MN là đường trung bình của hình thang ABCD)
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 8 tập 2 – Chân trời sáng tạo hoặc các đề thi thử Toán 8.
Bài 12 trang 85 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình thang cân và các tính chất của nó. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các bạn học sinh sẽ tự tin hơn khi làm bài tập Toán 8.