Chào mừng bạn đến với bài học về Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông trong chương trình Toán 8 - Chân trời sáng tạo tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn kiến thức cơ bản và quan trọng nhất về đồng dạng tam giác, đặc biệt là các trường hợp áp dụng cho tam giác vuông.
Chúng ta sẽ cùng nhau khám phá các định nghĩa, tính chất và các trường hợp đồng dạng thường gặp, cùng với các ví dụ minh họa cụ thể để bạn có thể hiểu rõ và áp dụng vào giải bài tập một cách hiệu quả.
Có các trườn hợp đồng dạng nào của hai tam giác vuông?
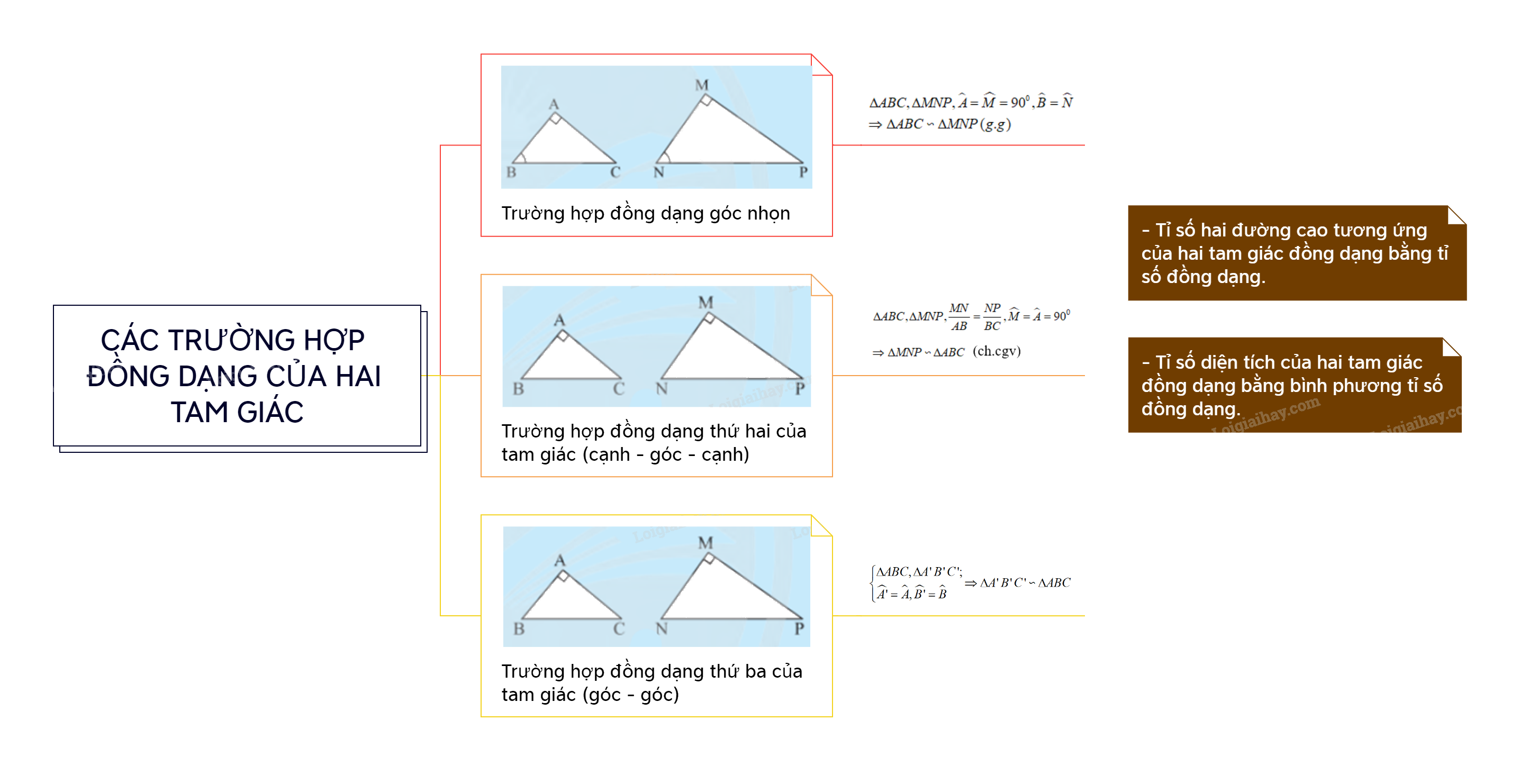
1. Trường hợp góc nhọn
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
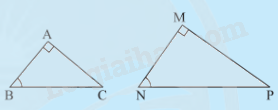
\(\begin{array}{l}\Delta ABC,\Delta MNP,\widehat A = \widehat M = {90^0},\widehat B = \widehat N\\ \Rightarrow \Delta ABC \backsim \Delta MNP\,(g.g)\end{array}\)
2. Trường hợp hai cạnh góc vuông
Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
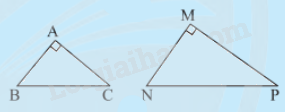
\(\Delta ABC,\Delta MNP,\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}},\widehat M = \widehat A = {90^0}\)
\( \Rightarrow \Delta MNP \backsim \Delta ABC\,\)(2cgv)
3. Trường hợp cạnh huyền cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng
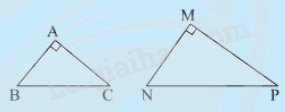
\(\Delta ABC,\Delta MNP,\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}},\widehat M = \widehat A = {90^0}\)
\( \Rightarrow \Delta MNP \backsim \Delta ABC\,\) (ch.cgv)
Chú ý:
- Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Trong chương trình Toán 8, kiến thức về tam giác đồng dạng đóng vai trò quan trọng, đặc biệt là các trường hợp đồng dạng của hai tam giác vuông. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo.
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ. Ký hiệu: △ABC ~ △A'B'C'.
Có ba trường hợp đồng dạng của hai tam giác vuông:
Nếu △ABC vuông tại A và △A'B'C' vuông tại A' có ∠B = ∠B' thì △ABC ~ △A'B'C'.
Nếu △ABC vuông tại A và △A'B'C' vuông tại A' có AB/A'B' = AC/A'C' thì △ABC ~ △A'B'C'.
Nếu △ABC vuông tại A và △A'B'C' vuông tại A' có BC/B'C' = AB/A'B' thì △ABC ~ △A'B'C'.
Các trường hợp đồng dạng của hai tam giác vuông được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tính độ dài đoạn thẳng, tính góc và chứng minh các mối quan hệ hình học.
Ví dụ 1: Cho △ABC vuông tại A và △A'B'C' vuông tại A' có ∠B = 60° và ∠B' = 60°. Chứng minh △ABC ~ △A'B'C'.
Giải: Vì △ABC và △A'B'C' đều là tam giác vuông và ∠B = ∠B' nên theo trường hợp 1, △ABC ~ △A'B'C'.
Ví dụ 2: Cho △ABC vuông tại A và △A'B'C' vuông tại A' có AB = 3cm, AC = 4cm, A'B' = 6cm, A'C' = 8cm. Chứng minh △ABC ~ △A'B'C'.
Giải: Ta có AB/A'B' = 3/6 = 1/2 và AC/A'C' = 4/8 = 1/2. Do đó, AB/A'B' = AC/A'C'. Theo trường hợp 2, △ABC ~ △A'B'C'.
Để củng cố kiến thức, bạn có thể thực hành giải các bài tập sau:
Khi áp dụng các trường hợp đồng dạng, cần xác định đúng các góc vuông, các cạnh tương ứng và đảm bảo các điều kiện của từng trường hợp được thỏa mãn.
Lý thuyết về các trường hợp đồng dạng của hai tam giác vuông là một phần kiến thức quan trọng trong chương trình Toán 8. Việc hiểu rõ và vận dụng linh hoạt các trường hợp này sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả và chính xác. Hãy luyện tập thường xuyên để nắm vững kiến thức này nhé!