Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 38 và 39 sách giáo khoa Toán 8 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập. Hãy cùng theo dõi và tham khảo lời giải dưới đây nhé!
Thay dấu bằng các dữ liệu thích hợp để hoàn thành lời giải bài toán. Một người đi xe gắn máy từ A đến B với tốc độ (40km/h). Lúc về người đó đi với tốc độ (50km/h) nên thời gian về ít hơn thời gian đi là (30) phút. Tìm chiều dài quãng đường AB.
Video hướng dẫn giải
Giải bài toán đã cho trong câu hỏi khởi động (trang 37)
Phương pháp giải:
Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau:
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
- Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Trả lời
- Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không.
- Kết luận.
Lời giải chi tiết:
Gọi giá tiền đôi giày lúc chưa giảm giá là \(x\) (đồng). Điều kiện: \(x > 0\).
Sau khi giảm giá \(15\% \) thì giá mới của đôi giày bằng \(85\% \) giá ban đầu của đôi giày. Ta có phương trình:
\(x.85\% = 1275000\)
\(x = 1275000:85\% \)
\(x = 1500000\) (thỏa mãn)
Vậy giá của đôi giày khi chưa giảm giá là 1 500 000 đồng.
Video hướng dẫn giải
Thay dấu ? bằng các dữ liệu thích hợp để hoàn thành lời giải bài toán.
Một người đi xe gắn máy từ A đến B với tốc độ \(40km/h\). Lúc về người đó đi với tốc độ \(50km/h\) nên thời gian về ít hơn thời gian đi là \(30\) phút. Tìm chiều dài quãng đường AB.
Giải
Gọi chiều dài quãng đường AB là \(x\left( {km} \right)\). Điều kiện ?
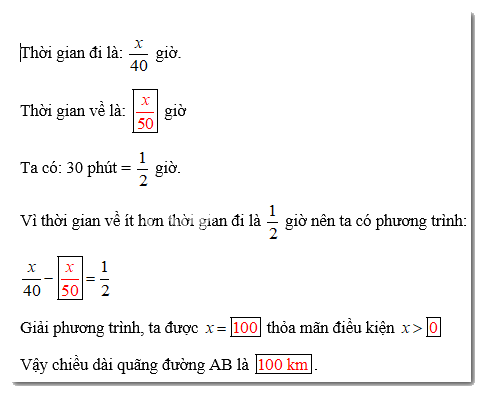
Thời gian đi là: \(\dfrac{x}{{40}}\) giờ.
Thời gian về là: ? giờ
Ta có: 30 phút = \(\dfrac{1}{2}\) giờ.
Vì thời gian về ít hơn thời gian đi là \(\dfrac{1}{2}\) giờ nên ta có phương trình:
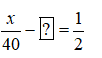
Giải phương trình, ta được x=? thỏa mãn điều kiện x> ?
Vậy chiều dài quãng đường AB là ?.
Phương pháp giải:
Quãng đường đi là một đại lượng dương.
Ta có công thức biểu diễn quãng đường, vận tốc, thời gian như sau:
\(s = vt\) với \(s\) là quãng đường; \(v\) là vận tốc; \(t\) là thời gian.
Lời giải chi tiết:
Video hướng dẫn giải
Một người mua 36 bông hoa hồng và bông hoa cẩm chướng hết tất cả 136 800 đồng. Giá mỗi bông hoa hồng là 3 000 đồng, giá mỗi bông hoa cẩm chướng là 4 800 đồng. Tính số bông hoa mỗi loại.

Phương pháp giải:
Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau:
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
- Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Trả lời
- Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không.
- Kết luận.
Lời giải chi tiết:
Gọi số bông hoa hồng đã mua là \(x\) (bông). Điều kiện: \(x \in {\mathbb{N}^*};x \le 36\)
Vì tổng số hoa người đó đã mua là 36 bông nên số bông hoa cẩm chướng người đó đã mua là: \(36 - x\)(bông).
Vì một bông hoa hồng có giá là 3 000 đồng nên số tiền mua hoa hồng là \(3000x\) đồng.
Vì một bông hoa cẩm chướng có giá là 4 800 đồng nên số tiền mua hoa cẩm chướng là \(\left( {36 - x} \right).4800\) (đồng).
Vì tổng số tiền mua 2 loại hoa là 136 800 đồng nên ta có phương trình:
\(3000x + \left( {36 - x} \right).4800 = 136800\)
\(3000x + 172800 - 4800x = 136800\)
\(3000x - 4800x = 136800 - 172800\)
\( - 1800x = - 3600\)
\(x = \left( { - 36000} \right):\left( { - 1800} \right)\)
\(x = 20\) (thỏa mãn điều kiện)
Vậy số bông hoa hồng đã mua là 20 bông; Số bông hoa cẩm chướng đã mua là \(36 - 20 = 16\) bông.
Video hướng dẫn giải
Thay dấu ? bằng các dữ liệu thích hợp để hoàn thành lời giải bài toán.
Một người đi xe gắn máy từ A đến B với tốc độ \(40km/h\). Lúc về người đó đi với tốc độ \(50km/h\) nên thời gian về ít hơn thời gian đi là \(30\) phút. Tìm chiều dài quãng đường AB.
Giải
Gọi chiều dài quãng đường AB là \(x\left( {km} \right)\). Điều kiện ?
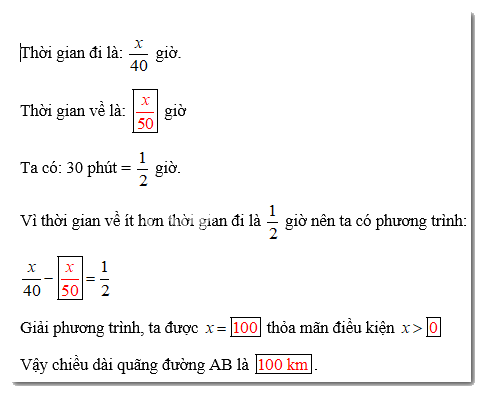
Thời gian đi là: \(\dfrac{x}{{40}}\) giờ.
Thời gian về là: ? giờ
Ta có: 30 phút = \(\dfrac{1}{2}\) giờ.
Vì thời gian về ít hơn thời gian đi là \(\dfrac{1}{2}\) giờ nên ta có phương trình:
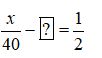
Giải phương trình, ta được x=? thỏa mãn điều kiện x> ?
Vậy chiều dài quãng đường AB là ?.
Phương pháp giải:
Quãng đường đi là một đại lượng dương.
Ta có công thức biểu diễn quãng đường, vận tốc, thời gian như sau:
\(s = vt\) với \(s\) là quãng đường; \(v\) là vận tốc; \(t\) là thời gian.
Lời giải chi tiết:
Video hướng dẫn giải
Một người mua 36 bông hoa hồng và bông hoa cẩm chướng hết tất cả 136 800 đồng. Giá mỗi bông hoa hồng là 3 000 đồng, giá mỗi bông hoa cẩm chướng là 4 800 đồng. Tính số bông hoa mỗi loại.

Phương pháp giải:
Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau:
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
- Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Trả lời
- Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không.
- Kết luận.
Lời giải chi tiết:
Gọi số bông hoa hồng đã mua là \(x\) (bông). Điều kiện: \(x \in {\mathbb{N}^*};x \le 36\)
Vì tổng số hoa người đó đã mua là 36 bông nên số bông hoa cẩm chướng người đó đã mua là: \(36 - x\)(bông).
Vì một bông hoa hồng có giá là 3 000 đồng nên số tiền mua hoa hồng là \(3000x\) đồng.
Vì một bông hoa cẩm chướng có giá là 4 800 đồng nên số tiền mua hoa cẩm chướng là \(\left( {36 - x} \right).4800\) (đồng).
Vì tổng số tiền mua 2 loại hoa là 136 800 đồng nên ta có phương trình:
\(3000x + \left( {36 - x} \right).4800 = 136800\)
\(3000x + 172800 - 4800x = 136800\)
\(3000x - 4800x = 136800 - 172800\)
\( - 1800x = - 3600\)
\(x = \left( { - 36000} \right):\left( { - 1800} \right)\)
\(x = 20\) (thỏa mãn điều kiện)
Vậy số bông hoa hồng đã mua là 20 bông; Số bông hoa cẩm chướng đã mua là \(36 - 20 = 16\) bông.
Video hướng dẫn giải
Giải bài toán đã cho trong câu hỏi khởi động (trang 37)
Phương pháp giải:
Giải bài toán bằng cách lập phương trình ta thực hiện 3 bước sau:
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
- Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: Trả lời
- Kiểm tra xem trong các nghiệm của phương trình , nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không.
- Kết luận.
Lời giải chi tiết:
Gọi giá tiền đôi giày lúc chưa giảm giá là \(x\) (đồng). Điều kiện: \(x > 0\).
Sau khi giảm giá \(15\% \) thì giá mới của đôi giày bằng \(85\% \) giá ban đầu của đôi giày. Ta có phương trình:
\(x.85\% = 1275000\)
\(x = 1275000:85\% \)
\(x = 1500000\) (thỏa mãn)
Vậy giá của đôi giày khi chưa giảm giá là 1 500 000 đồng.
Mục 2 của chương trình Toán 8 tập 2, Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về hình học, đặc biệt là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông. Các bài tập trong trang 38 và 39 SGK Toán 8 tập 2 yêu cầu học sinh vận dụng các kiến thức này để giải quyết các bài toán thực tế, chứng minh các đẳng thức hình học và tính toán các yếu tố liên quan đến hình.
Bài tập này yêu cầu học sinh nhắc lại các định nghĩa, tính chất của hình bình hành, các dấu hiệu nhận biết hình bình hành và các ứng dụng của chúng trong việc giải toán. Học sinh cần nắm vững các khái niệm cơ bản như cạnh đối song song, góc đối bằng nhau, đường chéo cắt nhau tại trung điểm và các tính chất liên quan đến diện tích hình bình hành.
Bài tập này tập trung vào việc ôn tập các tính chất của hình chữ nhật, bao gồm các góc vuông, các cạnh đối bằng nhau, các đường chéo bằng nhau và cắt nhau tại trung điểm. Học sinh cần hiểu rõ mối quan hệ giữa hình chữ nhật và hình bình hành, cũng như các ứng dụng của hình chữ nhật trong việc giải toán và thực tế.
Bài tập này yêu cầu học sinh ôn tập các tính chất của hình thoi, bao gồm các cạnh bằng nhau, các góc đối bằng nhau, các đường chéo vuông góc với nhau và cắt nhau tại trung điểm. Học sinh cần phân biệt hình thoi với hình bình hành và hình chữ nhật, cũng như các ứng dụng của hình thoi trong việc giải toán.
Bài tập này tập trung vào việc ôn tập các tính chất của hình vuông, bao gồm các cạnh bằng nhau, các góc vuông, các đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm. Học sinh cần hiểu rõ mối quan hệ giữa hình vuông và các hình bình hành khác, cũng như các ứng dụng của hình vuông trong việc giải toán và thực tế.
Bài tập: Cho hình bình hành ABCD, có góc A bằng 60 độ. Tính các góc còn lại của hình bình hành.
Lời giải:
Để học tốt môn Toán 8, các em cần thường xuyên luyện tập, làm bài tập đầy đủ và nắm vững các kiến thức cơ bản. Ngoài ra, các em có thể tham khảo các tài liệu tham khảo, các bài giảng online và các diễn đàn học tập để mở rộng kiến thức và trao đổi kinh nghiệm với bạn bè.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 38, 39 SGK Toán 8 tập 2, chương trình Chân trời sáng tạo. Chúc các em học tập tốt!