Bài 6 trang 76 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hình học, cụ thể là các kiến thức liên quan đến tứ giác. Bài tập này đòi hỏi học sinh phải vận dụng các định lý, tính chất đã học để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 76 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất,
Đề bài
Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3m và đặt cách xa tòa nhà 27m. Sau khi người ấy lùi xa cái cọc 1,2m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng năm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5m.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng các trường hợp đồng dạng của tam giác vuông và tính chất tam giác đồng dạng.
Lời giải chi tiết
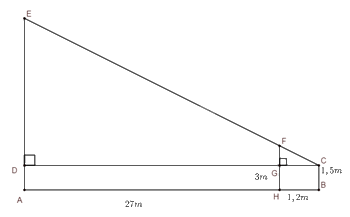
Giả sử, ta biểu diễn người quan sát, cái cọc, tòa nhà có dạng như hình vẽ.
Chiều cao người quan sát là \(CB = 1,5m\); chiều cao cái cọc là \(HF = 3m\); khoảng cách từ người đến cọc là \(HB = 1,2m\); khoảng cách từ tòa nhà đến cọc là \(AH = 27m\). Chiều cao tòa nhà là \(AE\).
Vì tứ giác \(GHBC\) là hình chữ nhật nên \(GC = HB = 1,2m\); Vì tứ giác \(GHAD\) là hình chữ nhật nên \(AH = DG = 27m;GH = AD = 1,5m\).
Chiều dài đoạn \(CD\) là: \(DC = DG + GC = 27 + 1,2 = 28,2m\).
Độ dài đoạn \(GF\) là: \(GF = FH - GH = 3 - 1,5 = 1,5m\)
Xét \(\Delta DEC\) và \(\Delta GFC\) có:
\(\widehat C\) chung
\(\widehat {EDC} = \widehat {FGC} = 90^\circ \)
Do đó, \(\Delta DEC\backsim\Delta GFC\) (g.g)
Vì \(\Delta DEC\backsim\Delta GFC\) nên \(\frac{{DC}}{{GC}} = \frac{{DE}}{{GF}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{28,2}}{{1,2}} = \frac{{DE}}{{1,5}} \Rightarrow DE = \frac{{28,2.1,5}}{{1,2}} = 35,25m\)
Chiều cao của tòa nhà là:
\(AD + DE = 35,25 + 1,5 = 36,75m\)
Vậy chiều cao tòa nhà là 36,75m.
Bài 6 trang 76 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về các loại tứ giác đặc biệt (hình bình hành, hình chữ nhật, hình thoi, hình vuông) và các tính chất liên quan đến đường trung bình của tam giác, đường trung bình của hình thang để giải quyết bài toán. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Đề bài cụ thể của bài 6 sẽ được trình bày đầy đủ tại đây)
Lời giải:
(Giải chi tiết từng bước của bài toán, kèm theo hình vẽ minh họa nếu cần thiết. Giải thích rõ ràng từng bước để học sinh dễ hiểu.)
Để giúp học sinh hiểu rõ hơn về cách giải bài 6 trang 76 SGK Toán 8 tập 2, chúng ta cùng xem xét một ví dụ minh họa sau:
(Trình bày một ví dụ tương tự bài 6, giải chi tiết và giải thích rõ ràng.)
Ngoài ra, các em học sinh có thể tham khảo thêm một số bài tập tương tự sau để rèn luyện kỹ năng:
(Cung cấp đáp án và hướng dẫn giải cho các bài tập tương tự.)
Khi giải các bài tập về tứ giác, học sinh cần lưu ý những điều sau:
Bài 6 trang 76 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hình học. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!