Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 82, 83, 84 sách giáo khoa Toán 8 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Dùng thước đo góc để đo số đo các góc
Video hướng dẫn giải
Tìm bốn ví dụ về hình chữ nhật trong thực tế
Phương pháp giải:
Áp dụng định nghĩa hình chữ nhật và ứng dụng vào thực tiễn tìm các ví dụ về hình chữ nhật
Lời giải chi tiết:
Các ví dụ về hình chữ nhật trong thực tế: Mặt bảng; ti vi; mặt bàn; khung ảnh
Video hướng dẫn giải
Dùng thước đo góc để đo số đo các góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) ở Hình 1 và rút ra nhận xét và số đo của chúng.

Phương pháp giải:
Dùng thước đo góc để đo số đo 4 góc của tứ giác rồi rút ra nhận xét.
Lời giải chi tiết:
Sau khi đo, ta thấy bốn góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) có số đo bằng nhau và bằng \(90^\circ \)
Video hướng dẫn giải
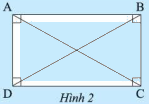
Cho \(ABCD\) là hình chữ nhật.
a) Chứng minh \(AB\) // \(CD\) và \(AD\) // \(BC\)
b) Tam giác \(ABD\) và tam giác \(BAC\) có bằng nhau không? Vì sao?
Phương pháp giải:
Áp dụng các tính chất của hình chữ nhật (cạnh, góc)
Lời giải chi tiết:
a) Vì \(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\), \(\widehat {DAB} = \widehat {ABC} = \widehat {DCB} = \widehat {ADC} = 90^\circ \)
Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ADC}}}\) (cmt)
\(BC = AD\) (gt)
Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c)
Suy ra \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) và \(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (hai cạnh tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\) // \(CD\); \(BC\) // \(AD\)
b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:
\(AB\) chung
\(\widehat {{\rm{BAD}}} = \widehat {{\rm{ABC}}}\) (cmt)
\(AD = BC\) (cmt)
Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)
Video hướng dẫn giải
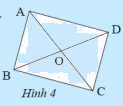
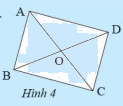
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Giải thích các khẳng định sau:
a) Nếu \(\widehat {{\rm{BAD}}}\) là góc vuông thì \(\widehat {{\rm{ADC}}}\) và \(\widehat {{\rm{ABC}}}\) cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {{\rm{BAD}}}\) vuông.
Phương pháp giải:
Áp dụng tính chất của hình bình hành
Lời giải chi tiết:
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\)
\(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\)
Nếu \(\widehat {{\rm{BAD}}} = 90^\circ \) suy ra \(AB \bot AD\)
Mà \(AB\) // \(CD\); \(AD\) // \(BC\)
Suy ra \(AD \bot CD;\;AB \bot BC\)
Suy ra \(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
b) Xét \(\Delta BAD\) và \(\Delta CDA\) ta có:
\(BA = CD\) (gt)
\(AD\) chung
\(BD = AC\) (gt)
Suy ra \(\Delta BAD = \Delta CDA\) (c-c-c)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{CDA}}}\) (hai góc tương ứng)
Mà \(\widehat {BAD} + \widehat {CDA} = 180^\circ \)(do \(AB\) // \(CD\) , cặp góc trong cùng phía)
Suy ra \(\widehat {BAD} = \widehat {CDA} = 90^\circ \)
Video hướng dẫn giải
Chỉ được sử dụng compa, hãy kiểm tra tứ giác có phải là hình chữ nhật hay không.
Phương pháp giải:
Sử dụng compa đo độ dài các cạnh, đường chéo
Lời giải chi tiết:
Gọi tứ giác trong hình là \(ABCD\)
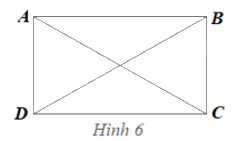
Sử dụng compa đo độ dài ta thu được \(AB = CD\); \(AD = BC\); \(AC = BD\)
Tứ giác \(ABCD\) ta có \(AB = CD\); \(AD = BC\) nên là hình bình hành
Hình bình hành \(ABCD\) có hai đường chéo \(AC = BD\) nên là hình chữ nhật
Video hướng dẫn giải
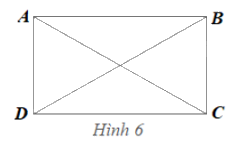
Cho biết \(a\), \(b\), \(d\) lần lượt là độ dài các cạnh và đường chéo của một hình chữ nhật. Thay dấu ? trong bảng sau bằng giá trị thích hợp.
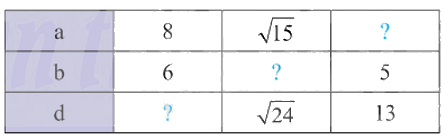
Phương pháp giải:
Áp dụng định lý Pythagore trong tam giác vuông
Lời giải chi tiết:
Giả sử \(ABCD\) là hình chữ nhật ; \(a\), \(b\), \(d\) lần lượt là độ dài của \(AB\), \(BC\), \(AC\)
Áp dụng định lý Pythagore vào \(\Delta ABC\) vuông tại \(B\) ta có:
\(A{C^2} = A{B^2} + B{C^2}\)
Do đó \({d^2} = {a^2} + {b^2}\) ; \({b^2} = {d^2} - {a^2}\); \({a^2} = {d^2} - {b^2}\)
Suy ra: \(d = \sqrt {{a^2} + {b^2}} \); \(b = \sqrt {{d^2} - {a^2}} \); \(a = \sqrt {{d^2} - {b^2}} \)
Với \(a = 8\); \(b = 6\) ta có: \(d = \sqrt {{8^2} + {6^2}} = \sqrt {64 + 36} = \sqrt {100} = 10\)
Với \(a = \sqrt {15} \); \(d = \sqrt {24} \) ta có: \(b = \sqrt {{{\sqrt {24} }^2} - {{\sqrt {15} }^2}} = \sqrt {24 - 15} = \sqrt 9 = 3\)
Với \(b = 5\); \(d = 13\) ta có: \(a = \sqrt {{{13}^2} - {5^2}} = \sqrt {169 - 25} = \sqrt {144} = 12\)

Video hướng dẫn giải
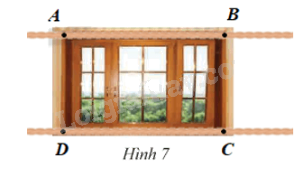
a) Hãy sử dụng ê ke sao cho chỉ sau ba lần đo ta có thể xác định khung cửa sổ ở Hình 7 có phải là hình chữ nhật hay không?
b) Hãy sử dụng một cuộn dây, xác định khung cửa sổ trong Hình 7 có là hình chữ nhật hay không?

Phương pháp giải:
a) Sử dụng ê ke đo 3 góc của tứ giác rồi tinh góc còn lại
b) Đo độ dài các cạnh, đường chéo
Lời giải chi tiết:
a) Sử dụng ê ke, ta thấy khung cửa có 3 góc vuông
Áp dụng tính chất tổng 4 góc trong tứ giác, suy ra góc còn lại cũng là góc vuông
Vậy khung cửa là hình chữ nhật
b)
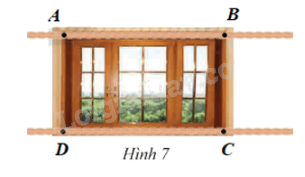
Sử dụng thước dây:
- Đo độ dài đoạn thẳng \(AB\) và đánh dấu 2 điểm trên đoạn dây (trùng với điểm \(A\), \(B\))
- Đặt một đầu đánh dấu trùng với điểm \(C\) và kiểm tra thấy điểm đánh dấu còn lại trùng với \(D\).
Vậy \(AB = CD\)
Thực hành tương tự ta có \(AD = BC\); \(AC = BD\)
Tứ giác \(ABCD\) có \(AB = CD\); \(AD = BC\) nên là hình bình hành
Mà \(AC = BD\) nên \(ABCD\) là hình chữ nhật
Vậy khung cửa có dạng hình chữ nhật
Video hướng dẫn giải
Dùng thước đo góc để đo số đo các góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) ở Hình 1 và rút ra nhận xét và số đo của chúng.

Phương pháp giải:
Dùng thước đo góc để đo số đo 4 góc của tứ giác rồi rút ra nhận xét.
Lời giải chi tiết:
Sau khi đo, ta thấy bốn góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) có số đo bằng nhau và bằng \(90^\circ \)
Video hướng dẫn giải
Cho \(ABCD\) là hình chữ nhật.
a) Chứng minh \(AB\) // \(CD\) và \(AD\) // \(BC\)
b) Tam giác \(ABD\) và tam giác \(BAC\) có bằng nhau không? Vì sao?
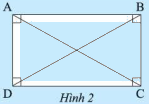
Phương pháp giải:
Áp dụng các tính chất của hình chữ nhật (cạnh, góc)
Lời giải chi tiết:
a) Vì \(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\), \(\widehat {DAB} = \widehat {ABC} = \widehat {DCB} = \widehat {ADC} = 90^\circ \)
Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(AB = CD\) (gt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ADC}}}\) (cmt)
\(BC = AD\) (gt)
Suy ra \(\Delta ABC = \Delta CDA\) (c-g-c)
Suy ra \(\widehat {{\rm{BAC}}} = \widehat {{\rm{ACD}}}\) và \(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (hai cạnh tương ứng)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\) // \(CD\); \(BC\) // \(AD\)
b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:
\(AB\) chung
\(\widehat {{\rm{BAD}}} = \widehat {{\rm{ABC}}}\) (cmt)
\(AD = BC\) (cmt)
Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)
Video hướng dẫn giải
Cho biết \(a\), \(b\), \(d\) lần lượt là độ dài các cạnh và đường chéo của một hình chữ nhật. Thay dấu ? trong bảng sau bằng giá trị thích hợp.
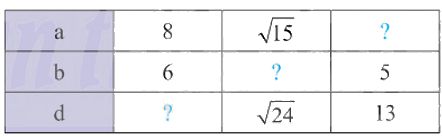
Phương pháp giải:
Áp dụng định lý Pythagore trong tam giác vuông
Lời giải chi tiết:
Giả sử \(ABCD\) là hình chữ nhật ; \(a\), \(b\), \(d\) lần lượt là độ dài của \(AB\), \(BC\), \(AC\)
Áp dụng định lý Pythagore vào \(\Delta ABC\) vuông tại \(B\) ta có:
\(A{C^2} = A{B^2} + B{C^2}\)
Do đó \({d^2} = {a^2} + {b^2}\) ; \({b^2} = {d^2} - {a^2}\); \({a^2} = {d^2} - {b^2}\)
Suy ra: \(d = \sqrt {{a^2} + {b^2}} \); \(b = \sqrt {{d^2} - {a^2}} \); \(a = \sqrt {{d^2} - {b^2}} \)
Với \(a = 8\); \(b = 6\) ta có: \(d = \sqrt {{8^2} + {6^2}} = \sqrt {64 + 36} = \sqrt {100} = 10\)
Với \(a = \sqrt {15} \); \(d = \sqrt {24} \) ta có: \(b = \sqrt {{{\sqrt {24} }^2} - {{\sqrt {15} }^2}} = \sqrt {24 - 15} = \sqrt 9 = 3\)
Với \(b = 5\); \(d = 13\) ta có: \(a = \sqrt {{{13}^2} - {5^2}} = \sqrt {169 - 25} = \sqrt {144} = 12\)

Video hướng dẫn giải
Tìm bốn ví dụ về hình chữ nhật trong thực tế
Phương pháp giải:
Áp dụng định nghĩa hình chữ nhật và ứng dụng vào thực tiễn tìm các ví dụ về hình chữ nhật
Lời giải chi tiết:
Các ví dụ về hình chữ nhật trong thực tế: Mặt bảng; ti vi; mặt bàn; khung ảnh
Video hướng dẫn giải
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Giải thích các khẳng định sau:
a) Nếu \(\widehat {{\rm{BAD}}}\) là góc vuông thì \(\widehat {{\rm{ADC}}}\) và \(\widehat {{\rm{ABC}}}\) cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {{\rm{BAD}}}\) vuông.
Phương pháp giải:
Áp dụng tính chất của hình bình hành
Lời giải chi tiết:
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\)
\(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\)
Nếu \(\widehat {{\rm{BAD}}} = 90^\circ \) suy ra \(AB \bot AD\)
Mà \(AB\) // \(CD\); \(AD\) // \(BC\)
Suy ra \(AD \bot CD;\;AB \bot BC\)
Suy ra \(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
b) Xét \(\Delta BAD\) và \(\Delta CDA\) ta có:
\(BA = CD\) (gt)
\(AD\) chung
\(BD = AC\) (gt)
Suy ra \(\Delta BAD = \Delta CDA\) (c-c-c)
Suy ra \(\widehat {{\rm{BAD}}} = \widehat {{\rm{CDA}}}\) (hai góc tương ứng)
Mà \(\widehat {BAD} + \widehat {CDA} = 180^\circ \)(do \(AB\) // \(CD\) , cặp góc trong cùng phía)
Suy ra \(\widehat {BAD} = \widehat {CDA} = 90^\circ \)
Video hướng dẫn giải
Chỉ được sử dụng compa, hãy kiểm tra tứ giác có phải là hình chữ nhật hay không.
Phương pháp giải:
Sử dụng compa đo độ dài các cạnh, đường chéo
Lời giải chi tiết:
Gọi tứ giác trong hình là \(ABCD\)
Sử dụng compa đo độ dài ta thu được \(AB = CD\); \(AD = BC\); \(AC = BD\)
Tứ giác \(ABCD\) ta có \(AB = CD\); \(AD = BC\) nên là hình bình hành
Hình bình hành \(ABCD\) có hai đường chéo \(AC = BD\) nên là hình chữ nhật
Video hướng dẫn giải
a) Hãy sử dụng ê ke sao cho chỉ sau ba lần đo ta có thể xác định khung cửa sổ ở Hình 7 có phải là hình chữ nhật hay không?
b) Hãy sử dụng một cuộn dây, xác định khung cửa sổ trong Hình 7 có là hình chữ nhật hay không?

Phương pháp giải:
a) Sử dụng ê ke đo 3 góc của tứ giác rồi tinh góc còn lại
b) Đo độ dài các cạnh, đường chéo
Lời giải chi tiết:
a) Sử dụng ê ke, ta thấy khung cửa có 3 góc vuông
Áp dụng tính chất tổng 4 góc trong tứ giác, suy ra góc còn lại cũng là góc vuông
Vậy khung cửa là hình chữ nhật
b)
Sử dụng thước dây:
- Đo độ dài đoạn thẳng \(AB\) và đánh dấu 2 điểm trên đoạn dây (trùng với điểm \(A\), \(B\))
- Đặt một đầu đánh dấu trùng với điểm \(C\) và kiểm tra thấy điểm đánh dấu còn lại trùng với \(D\).
Vậy \(AB = CD\)
Thực hành tương tự ta có \(AD = BC\); \(AC = BD\)
Tứ giác \(ABCD\) có \(AB = CD\); \(AD = BC\) nên là hình bình hành
Mà \(AC = BD\) nên \(ABCD\) là hình chữ nhật
Vậy khung cửa có dạng hình chữ nhật
Mục 1 của chương trình Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa các kiến thức về số hữu tỉ, số thực, biểu thức đại số và các phép toán cơ bản. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập 1 thường yêu cầu học sinh thực hiện các phép tính với số hữu tỉ, số thực. Để giải bài tập này, các em cần nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ, số thực và thứ tự thực hiện các phép toán.
Bài tập 2 thường liên quan đến việc tìm giá trị của biểu thức đại số. Để giải bài tập này, các em cần thay các giá trị đã cho vào biểu thức và thực hiện các phép tính.
Bài tập 3 thường yêu cầu học sinh giải các bài toán thực tế liên quan đến số hữu tỉ, số thực. Để giải bài tập này, các em cần phân tích đề bài, xác định các yếu tố liên quan và sử dụng các kiến thức đã học để giải quyết vấn đề.
Ví dụ: Một cửa hàng bán một chiếc áo với giá gốc là 150.000 đồng. Cửa hàng giảm giá 10% cho chiếc áo đó. Hỏi giá bán chiếc áo sau khi giảm giá là bao nhiêu? Giải: Số tiền giảm giá là 150.000 * 10% = 15.000 đồng. Giá bán chiếc áo sau khi giảm giá là 150.000 - 15.000 = 135.000 đồng.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em sẽ học tốt môn Toán 8 và đạt kết quả cao trong học tập. Chúc các em thành công!