Bài 3 trang 87 SGK Toán 8 tập 1 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh áp dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 87 SGK Toán 8 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác
Đề bài
Cho tam giác \(ABC\) có đường cao \(AH\). Gọi \(I\) là trung điểm của \(AC\), \(E\) là điểm đối xứng với \(H\) qua \(I\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(HC\), \(CE\). Các đường thẳng \(AM\), \(AN\) cắt \(HE\) tại \(G\) và \(K\).
a) Chứng minh tứ giác \(AHCE\) là hình chữ nhật
b) Chứng minh \(HG = GK = KE\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Áp dụng các dấu hiệu nhận biết của hình chữ nhật
b) Áp dụng tính chất trọng tâm của tam giác
Lời giải chi tiết
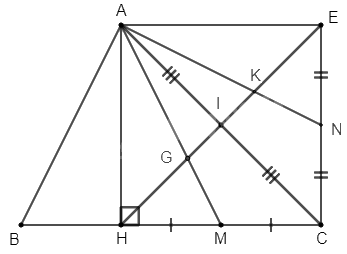
a) Do \(E\) là điểm đối xứng với \(H\) qua \(I\) nên \(I\) là trung điểm của \(HE\) hay \(HI = EI\)
Tứ giác \(AHCE\) có hai đường chéo \(AC\) và \(HE\) cắt nhau tại trung điểm \(I\) (gt) nên là hình bình hành.
Lại có \(\widehat {AHC} = 90^\circ \) (do \(AH\) là đường cao) nên hình bình hành \(AHCE\) là hình chữ nhật.
b) Xét \(\Delta AHC\) có \(AM\), \(HI\) là hai đường trung tuyến cắt nhau tại \(G\) nên \(G\) là trọng tâm của \(\Delta AHC\).
Suy ra: \(HG = \frac{2}{3}HI;\;IG = \frac{1}{2}HG\)
Chứng minh tưng tự đối với \(\Delta AEC\) có \(K\) là trọng tâm của \(\Delta AEC\)
Suy ra: \(EK = \frac{2}{3}EI\) và \(IK = \frac{1}{2}EK\)
Ta có: \(HG = \frac{2}{3}HI;\;EK = \frac{2}{3}EI\) mà \(HI = EI\)
Suy ra \(HG = EK = \frac{2}{3}EI\)
Mà \(EI = \frac{1}{2}EH\)
Suy ra \(HG = EK = \frac{1}{3}HE\)
Suy ra \(GK = HE - HG - KE = HE - \frac{1}{3}HE - \frac{1}{3}HE = \frac{1}{3}HE\)
Vậy \(HG = GK = KE\)
Bài 3 trang 87 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về đa thức, các phép toán trên đa thức và các hằng đẳng thức đáng nhớ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp giải quyết bài toán.
Bài 3 yêu cầu học sinh thực hiện các phép tính đa thức, thường bao gồm các phép cộng, trừ, nhân, chia đa thức. Đôi khi, bài tập còn yêu cầu học sinh phân tích đa thức thành nhân tử hoặc rút gọn biểu thức đa thức.
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau đi qua lời giải chi tiết của từng phần:
Để thực hiện phép tính này, chúng ta sử dụng công thức phân phối (A + B)(C – D) = AC – AD + BC – BD:
(2x + 3)(x – 1) = 2x(x – 1) + 3(x – 1) = 2x2 – 2x + 3x – 3 = 2x2 + x – 3
Tương tự như phần a, chúng ta sử dụng công thức phân phối:
(x – 2)(x2 + 3x – 1) = x(x2 + 3x – 1) – 2(x2 + 3x – 1) = x3 + 3x2 – x – 2x2 – 6x + 2 = x3 + x2 – 7x + 2
Đây là một trường hợp đặc biệt, chúng ta có thể sử dụng hằng đẳng thức (a + b)(a2 – ab + b2) = a3 + b3:
(x + 1)(x2 – x + 1) = x3 + 13 = x3 + 1
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự sau:
Bài 3 trang 87 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép toán trên đa thức. Bằng cách nắm vững các khái niệm cơ bản, phương pháp giải quyết bài toán và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
Trong quá trình giải bài tập, học sinh cần chú ý:
Học sinh có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về đa thức và các phép toán trên đa thức: