Giải Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo

Bài 12 trang 56 SGK Toán 8 tập 1 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh áp dụng các kiến thức đã học để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Một bể kính hình hộp chữ nhật chứa nước có hai cạnh đáy là (50)cm và (40)cm

Đề bài

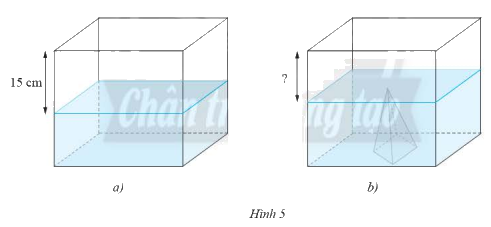
Một bể kính hình hộp chữ nhật chứa nước có hai cạnh đáy là \(50\)cm và \(40\)cm, khoảng cách từ mực nước tới miệng bể là \(15\)cm. Người ta dự định đặt vào bể một khối đá hình chóp tứ giác đều cạnh đáy là \(20\)cm, chiều cao \(15\)cm. Khi đó khoảng cách mực nước tới miệng bể là bao nhiêu? Biết rằng bề dày của đáy bể và thành bể không đáng kể, sau khi đặt khối đá vào, nước ngập khối đá và không tràn ra ngoài.

Giải Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo 2

- Tính lượng nước cần đổ vào bể để bể chứa đầy nước

- Tính thể tích khối đá

- Tính lượng nước cần đổ vào bể (sau khi có khối đá) để bể chứa đầy nước

- Tính khoảng cách mực nước tới miệng bể

Lời giải chi tiết

Lượng nước cần đổ vào bể để bể chứa đầy nước là:

\(50.40.15 = 30000\) (\(c{m^3}\))

Thể tích khối đá là: \(\frac{1}{3}.20.20.15 = 2000\) (\(c{m^3}\))

Lượng nước cần đổ vào bể (sau khi có khối đá) để bể chứa đầy nước là:

\(30000 - 2000 = 28000\) (\(c{m^3}\))

Khoảng cách mực nước tới miệng bể là: \(28000:50:40 = 14\) (cm)

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo đặc sắc thuộc chuyên mục sgk toán 8 trên môn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo: Tóm tắt lý thuyết và phương pháp giải

Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số, đặc biệt là các quy tắc cộng, trừ, nhân, chia đa thức để giải quyết bài toán. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như đơn thức, đa thức, bậc của đa thức, hệ số của đa thức, và các phép toán trên đa thức.

Phân tích đề bài và xác định yêu cầu

Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán. Xác định rõ các đại lượng đã cho và đại lượng cần tìm. Phân tích mối quan hệ giữa các đại lượng này để tìm ra phương pháp giải phù hợp.

Lời giải chi tiết Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo

(Nội dung lời giải chi tiết bài tập sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, giải thích rõ ràng từng bước, và sử dụng các ký hiệu toán học chính xác. Ví dụ:)

Bước 1: Biến đổi biểu thức A bằng cách sử dụng quy tắc nhân đa thức với đa thức.
Bước 2: Thu gọn biểu thức A bằng cách cộng các đơn thức đồng dạng.
Bước 3: Thay giá trị của x và y vào biểu thức A đã thu gọn để tính giá trị của biểu thức.
Bước 4: Kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa và bài tập tương tự

Để giúp học sinh hiểu rõ hơn về phương pháp giải bài tập này, chúng ta sẽ xem xét một ví dụ minh họa:

Ví dụ: Cho biểu thức A = (x + y)(x - y) + x². Hãy thu gọn biểu thức A.

Lời giải:

A = (x + y)(x - y) + x² = x² - y² + x² = 2x² - y²

Ngoài ra, chúng ta có thể giải một số bài tập tương tự để rèn luyện kỹ năng:

Bài tập 1: Thu gọn biểu thức B = (2x + 1)(2x - 1) + 4x²
Bài tập 2: Tính giá trị của biểu thức C = (x + 2)(x - 2) - x² khi x = 3

Lưu ý quan trọng khi giải bài tập

Khi giải bài tập về các phép biến đổi đại số, học sinh cần lưu ý một số điểm sau:

Luôn kiểm tra lại kết quả sau khi giải xong để đảm bảo tính chính xác.
Sử dụng các quy tắc biến đổi đại số một cách chính xác.
Chú ý đến dấu của các số hạng trong biểu thức.
Rèn luyện kỹ năng biến đổi đại số thường xuyên để nâng cao khả năng giải quyết bài tập.

Ứng dụng của kiến thức vào thực tế

Kiến thức về các phép biến đổi đại số có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như khoa học, kỹ thuật, kinh tế, và tài chính. Ví dụ, trong khoa học, các phép biến đổi đại số được sử dụng để xây dựng các mô hình toán học mô tả các hiện tượng tự nhiên. Trong kỹ thuật, các phép biến đổi đại số được sử dụng để thiết kế các hệ thống và thiết bị. Trong kinh tế và tài chính, các phép biến đổi đại số được sử dụng để phân tích dữ liệu và đưa ra các quyết định đầu tư.

Tổng kết

Bài 12 trang 56 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bằng cách nắm vững các khái niệm cơ bản, phân tích đề bài một cách cẩn thận, và áp dụng các quy tắc biến đổi đại số một cách chính xác, học sinh có thể giải quyết bài tập này một cách hiệu quả. Hy vọng rằng lời giải chi tiết và các ví dụ minh họa trong bài viết này sẽ giúp các em học sinh học tập tốt hơn môn Toán 8.