Chào mừng bạn đến với bài học về Lý thuyết Mô tả xác suất bằng tỉ số trong chương trình Toán 8 - Chân trời sáng tạo tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về xác suất, giúp bạn tự tin giải quyết các bài toán liên quan.
Chúng ta sẽ cùng nhau khám phá khái niệm xác suất, cách tính xác suất của một sự kiện đơn giản, và ứng dụng của xác suất trong thực tế.
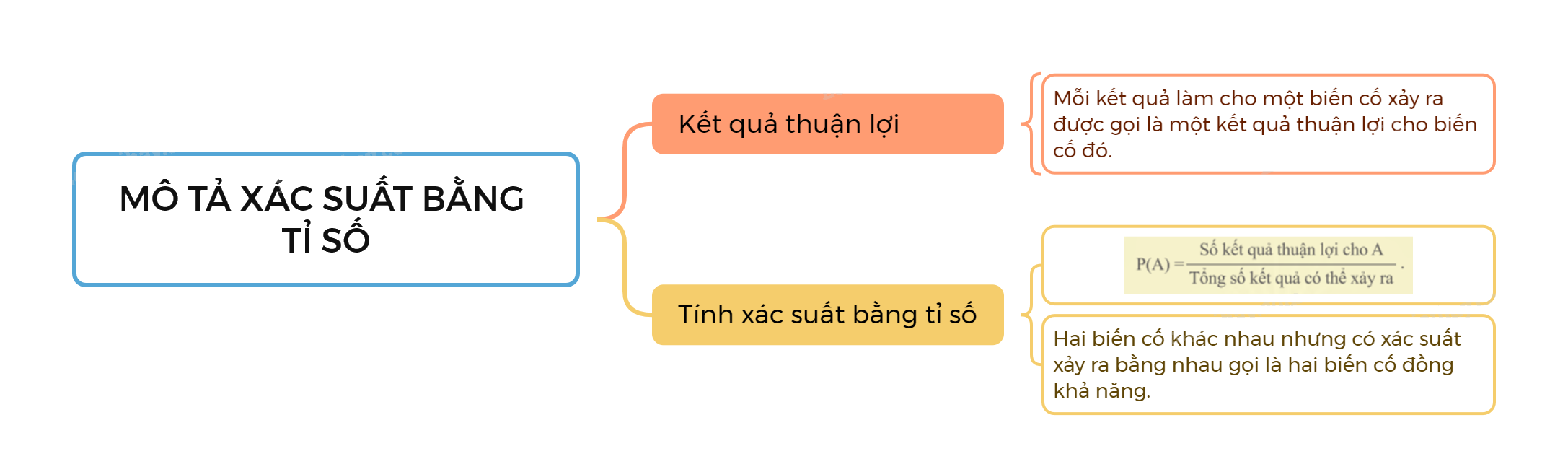
Mô tả xác suất bằng tỉ số như thế nào?
1. Kết quả thuận lợi
Trong một phép thử, mỗi kết quả làm cho một biến cố xảy ra được gọi là một kết quả thuận lợi cho biến cố đó.
2. Mô tả xác suất bằng tỉ số
Khi tất cả các kết quả của một trò chơi hay phép thử nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra của biến cố A là tỉ số giữa số kết quả thuận lợi của A và tổng số kết quả có thể xảy ra của phép thử, tức là

Chú ý: Nếu A và B là hai biến cố khác nhau nhưng có xác suất xảy ra bằng nhau thì ta nói A và B là hai biến cố đồng khả năng.
Ví dụ: Gieo một con xúc xắc.
Các kết quả có thể của hành động trên là 1, 2, 3, 4, 5, 6 chấm. Có 6 kết quả có thể.
Biến cố A: “Gieo được số chấm lẻ” xảy ra khi gieo được các số lẻ. Do đó các kết quả thuận lợi cho biến cố A là 1, 3, 5. Có 3 kết quả thuận lợi
Xác suất của biến cố A là: \(P(A) = \frac{3}{6} = \frac{1}{2}\)
Xác suất là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống. Trong chương trình Toán 8, học sinh bắt đầu làm quen với khái niệm này thông qua việc tìm hiểu về mô tả xác suất bằng tỉ số.
Xác suất của một sự kiện là khả năng sự kiện đó xảy ra. Nó được biểu diễn bằng một số thực nằm trong khoảng từ 0 đến 1. Xác suất bằng 0 có nghĩa là sự kiện không thể xảy ra, xác suất bằng 1 có nghĩa là sự kiện chắc chắn xảy ra.
Để tính xác suất của một sự kiện đơn giản, ta sử dụng công thức:
P(A) = n(A) / n(Ω)
Trong đó:
Ví dụ 1: Gieo một con xúc xắc 6 mặt. Tính xác suất để mặt xuất hiện là số lẻ.
Giải:
Ví dụ 2: Trong một hộp có 5 quả bóng màu đỏ và 3 quả bóng màu xanh. Lấy ngẫu nhiên một quả bóng. Tính xác suất để quả bóng được lấy ra là màu đỏ.
Giải:
Hãy tự giải các bài tập sau để củng cố kiến thức:
Ngoài việc tính xác suất của các sự kiện đơn giản, ta còn có thể tính xác suất của các sự kiện phức tạp hơn, chẳng hạn như xác suất của sự kiện hợp, xác suất của sự kiện giao, và xác suất có điều kiện. Những kiến thức này sẽ được học trong các lớp toán cao hơn.
Lý thuyết về mô tả xác suất bằng tỉ số là một phần quan trọng của chương trình Toán 8. Việc nắm vững kiến thức này sẽ giúp bạn hiểu rõ hơn về khái niệm xác suất và ứng dụng của nó trong thực tế. Hãy luyện tập thường xuyên để củng cố kiến thức và tự tin giải quyết các bài toán liên quan.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích. Chúc bạn học tốt!