Bài 4 trang 91 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hình học, cụ thể là các kiến thức liên quan đến tứ giác. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để chứng minh hoặc tính toán các yếu tố của tứ giác.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 91 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:
Đề bài
Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:
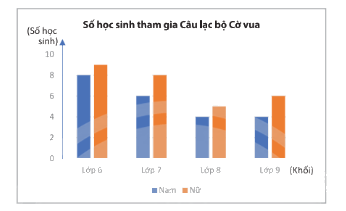
Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất các biến cố:
\(A\): “Học sinh được chọn là nữ”.
\(B\): “Học sinh được chọn học lớp 8”.
\(C\): “Học sinh được chọn là nam và không học lớp 7”.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Khi tất cả các kết quả của một trò chơi hay phép thử ngẫu nghiệm đều có khả năng xảy ra bằng nhau thì xác suất xảy ra biến cố \(A\) là tỉ số giữ số kết quả thuận lời cho \(A\) và tổng số kết quả có thể xảy ra của phép thử, tức là:
\(P\left( A \right) = \)Số kết quả thuận lợi : Số kết quả có thể xảy ra.
Lời giải chi tiết
Tổng số học sinh tham gia câu lạc bộ là:
\(8 + 9 + 6 + 8 + 4 + 5 + 4 + 6 = 50\) (học sinh)
- Biến cố \(A\) xảy ra khi bạn học sinh chọn được là nữ.
Số học sinh nữ tham gia câu lạc bộ là:
\(9 + 8 + 5 + 6 = 28\) (học sinh)
Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{{28}}{{50}} = \frac{{14}}{{25}}\)
- Biến cố \(B\) xảy ra khi bạn học sinh chọn được là học sinh lớp 8.
Số học sinh lớp 8 trong câu lạc bộ là:
\(4 + 5 = 9\)(học sinh)
Xác suất của biến có \(B\) là:
\(P\left( B \right) = \frac{9}{{50}}\)
- Biến cố \(C\) xảy ra khi bạn học sinh chọn được là nam và không học lớp 7.
Số học sinh câu lạc bộ là nam và không học lớp 7 là:
\(8 + 4 + 4 = 16\)
Xác suất của biến có \(C\) là:
\(P\left( C \right) = \frac{{16}}{{50}} = \frac{8}{{25}}\)
Bài 4 trang 91 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh giải quyết một bài toán liên quan đến tứ giác, cụ thể là việc chứng minh một tứ giác là hình bình hành. Để giải bài toán này, học sinh cần nắm vững các kiến thức về:
Trước khi bắt tay vào giải bài toán, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và các dữ kiện đã cho. Sau đó, học sinh cần phân tích bài toán để tìm ra hướng giải phù hợp. Thông thường, để chứng minh một tứ giác là hình bình hành, học sinh cần chứng minh một trong các dấu hiệu nhận biết hình bình hành.
Đề bài: (Giả sử đề bài cụ thể của bài 4 trang 91 SGK Toán 8 tập 2 – Chân trời sáng tạo được đưa ra ở đây. Ví dụ: Cho tứ giác ABCD có AB song song CD và AD song song BC. Chứng minh ABCD là hình bình hành.)
Lời giải:
Khi giải bài tập về tứ giác, học sinh cần chú ý:
Ngoài bài 4 trang 91 SGK Toán 8 tập 2 – Chân trời sáng tạo, học sinh có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập về tứ giác.
Kiến thức về tứ giác có ứng dụng rộng rãi trong thực tế, ví dụ như trong kiến trúc, xây dựng, thiết kế đồ họa,… Việc hiểu rõ về tứ giác giúp chúng ta giải quyết các vấn đề thực tế một cách hiệu quả.
Để củng cố kiến thức, các em có thể thử giải các bài tập sau:
Bài 4 trang 91 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hình học. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, các em học sinh sẽ tự tin hơn trong việc học Toán 8.