Bài 2 trang 57 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh áp dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 57 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tam giác
Đề bài
Tam giác \(ABC\) có \(AB = 6cm,AC = 8cm,BC = 10cm\). Đường phân giác của góc \(BAC\) cắt cạnh \(BC\) tại \(D\).
a) Tính độ dài các đoạn thẳng \(DB\) và \(DC\).
b) Tính tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Sử dụng Tính chất đường phân giác trong tam giác:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
- Diện tích tam giác
\(S = \frac{1}{2}a.h\) với \(a\) là độ dài đáy và \(h\) là chiều cao.
Lời giải chi tiết
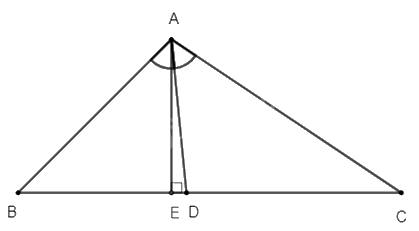
a) Ta có: \(BD + DC = BC \) suy ra \(DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \)
\(\frac{{BD}}{{10 - BD}} = \frac{6}{8} \)
\(8BD = 6.\left( {10 - BD} \right) \)
\(8BD = 60 - 6BD\)
\(8BD + 6BD = 60 \)
\(14BD = 60 \)
\(BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\(DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC\), ta có \(AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \) nên \(AE \bot BD \) suy ra \(AE\) là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \) nên \(AE \bot DC \) suy ra \(AE\) là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).
Bài 2 trang 57 SGK Toán 8 tập 2 – Chân trời sáng tạo thường xoay quanh việc áp dụng các quy tắc về phép nhân đa thức, phép chia đa thức và các hằng đẳng thức đáng nhớ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để cung cấp lời giải chính xác, chúng ta cần biết nội dung cụ thể của bài 2 trang 57. Tuy nhiên, dựa trên cấu trúc chung của sách Toán 8 Chân trời sáng tạo, bài tập này có thể thuộc một trong các dạng sau:
Bài tập yêu cầu thực hiện các phép tính với đa thức, ví dụ:
(2x + 3)(x - 1) - (x + 2)^2
Cách giải:
Ví dụ:
(2x + 3)(x - 1) - (x + 2)^2 = (2x^2 - 2x + 3x - 3) - (x^2 + 4x + 4) = 2x^2 + x - 3 - x^2 - 4x - 4 = x^2 - 3x - 7
Bài tập yêu cầu phân tích một đa thức thành nhân tử, ví dụ:
x^2 - 4x + 4
Cách giải:
Ví dụ:
x^2 - 4x + 4 = (x - 2)^2
Bài tập yêu cầu tìm giá trị của x thỏa mãn một phương trình, ví dụ:
2x - 5 = 3
Cách giải:
Ví dụ:
2x - 5 = 3 => 2x = 8 => x = 4
Ngoài SGK Toán 8 tập 2 – Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em học sinh sẽ tự tin hơn trong việc giải bài 2 trang 57 SGK Toán 8 tập 2 – Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.