Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 71 SGK Toán 8 – Chân trời sáng tạo. Bài viết này sẽ giúp các em hiểu rõ cách giải bài tập, nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp đáp án chính xác, phương pháp giải dễ hiểu và nhiều tài liệu học tập hữu ích khác.
Tìm
Đề bài
Tìm \(x\) và \(y\) ở các hình sau.
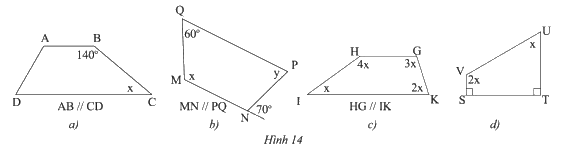
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hai đường thẳng song song, định lý tổng bốn góc trong tứ gíac
Lời giải chi tiết
a) Vì \(AB\) // \(CD\) (gt) suy ra:
\(\widehat B + \widehat C = 180^\circ \) (cặp góc trong cùng phía)
\(\begin{array}{l}140^\circ + x = 180^\circ \\x = 40^\circ \end{array}\)
b) Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat M + \widehat Q = 180^\circ \) (trong cùng phía)
\(\begin{array}{l}x + 60^\circ = 180^\circ \\x = 120^\circ \end{array}\)
Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow y = \widehat P = \widehat N = 70^\circ \) (so le trong)
c) Xét tứ giác \(IHGK\) ta có:
\(\begin{array}{l}\widehat H + \widehat G + \widehat I + \widehat K = 360^\circ \\4x + 3x + 2x + x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10 = 36^\circ \end{array}\)
d) Xét tứ giác \(UVST\) ta có:
\(\widehat U + \widehat V + \widehat S + \widehat T = 360^\circ \)
\(\begin{array}{l}x + 2x + 90^\circ + 90^\circ = 360^\circ \\3x + 180^\circ = 360^\circ \\3x = 180^\circ \\x = 60^\circ \end{array}\)
Bài 1 trang 71 SGK Toán 8 – Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 1 yêu cầu chúng ta tính toán các yếu tố của hình hộp chữ nhật và hình lập phương dựa trên các thông tin đã cho. Dưới đây là hướng dẫn giải chi tiết từng phần của bài tập:
Để tính diện tích xung quanh của hình hộp chữ nhật, ta sử dụng công thức: Diện tích xung quanh = 2 * (chiều dài + chiều rộng) * chiều cao. Trong bài toán, ta cần xác định chính xác chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật từ dữ liệu đề bài.
Diện tích toàn phần của hình hộp chữ nhật được tính bằng công thức: Diện tích toàn phần = Diện tích xung quanh + 2 * Diện tích đáy. Ta cần tính diện tích đáy của hình hộp chữ nhật trước khi áp dụng công thức này.
Thể tích của hình hộp chữ nhật được tính bằng công thức: Thể tích = chiều dài * chiều rộng * chiều cao. Việc xác định đúng các kích thước là yếu tố quan trọng để có kết quả chính xác.
Diện tích toàn phần của hình lập phương được tính bằng công thức: Diện tích toàn phần = 6 * cạnh2. Ta cần xác định độ dài cạnh của hình lập phương từ dữ liệu đề bài.
Thể tích của hình lập phương được tính bằng công thức: Thể tích = cạnh3. Việc tính toán chính xác cạnh là yếu tố then chốt để có kết quả đúng.
Giả sử, một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Hãy tính:
Để củng cố kiến thức và kỹ năng giải bài tập về hình hộp chữ nhật và hình lập phương, các em có thể luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc thực hành thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi giải các bài toán khó.
Khi giải các bài tập về hình học, các em nên vẽ hình để dễ dàng hình dung và xác định các yếu tố cần thiết. Ngoài ra, hãy đọc kỹ đề bài và xác định rõ yêu cầu của bài toán trước khi bắt đầu giải. Chúc các em học tập tốt!
| Hình | Công thức |
|---|---|
| Hình hộp chữ nhật | Diện tích xung quanh = 2 * (dài + rộng) * cao |
| Hình hộp chữ nhật | Diện tích toàn phần = Diện tích xung quanh + 2 * Diện tích đáy |
| Hình hộp chữ nhật | Thể tích = dài * rộng * cao |
| Hình lập phương | Diện tích toàn phần = 6 * cạnh2 |
| Hình lập phương | Thể tích = cạnh3 |