Giải bài 7 trang 67 SGK Toán 8 – Chân trời sáng tạo

Bài 7 trang 67 SGK Toán 8 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các tình huống khác.

Trên bản đồ, tứ giác

Đề bài

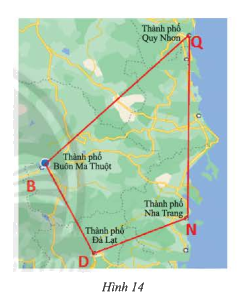
Trên bản đồ, tứ giác \(BDNQ\) với các đỉnh là các thành phố Buôn Ma Thuột, Đà Lạt, Nha Trang, Quy Nhơn.

a) Tìm các cạnh kề và cạnh đối diện của cạnh \(BD\).

b) Tìm các đường chéo của tứ giác

Giải bài 7 trang 67 SGK Toán 8 – Chân trời sáng tạo 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài 7 trang 67 SGK Toán 8 – Chân trời sáng tạo 2

Sử dụng kiến thức về đặc điểm của tứ giác để trả lời các câu hỏi

Lời giải chi tiết

a) Các cạnh kề của \(BD\) là: \(BQ\), \(DN\)

Cạnh đối của cạnh \(BD\) là: \(NQ\)

b) Các đường chéo của tứ giác là: \(BN;\;DQ\)

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 7 trang 67 SGK Toán 8 – Chân trời sáng tạo đặc sắc thuộc chuyên mục sgk toán 8 trên toán math. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 7 trang 67 SGK Toán 8 – Chân trời sáng tạo: Phân tích và Hướng dẫn Giải Chi Tiết

Bài 7 trang 67 SGK Toán 8 – Chân trời sáng tạo yêu cầu học sinh thực hiện các phép biến đổi đại số để rút gọn biểu thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về dấu ngoặc, quy tắc chuyển vế, và các phép toán cơ bản.

Nội dung bài toán

Bài toán cụ thể yêu cầu học sinh rút gọn biểu thức sau: (3x + 5)(2x - 1) - 5x(x - 3)

Phương pháp giải

Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:

Bước 1: Phân phối (nhân) các số hạng trong ngoặc.
Bước 2: Thu gọn các số hạng đồng dạng.
Bước 3: Viết kết quả cuối cùng.

Giải chi tiết

(3x + 5)(2x - 1) - 5x(x - 3)

Bước 1: Phân phối

= (3x * 2x) + (3x * -1) + (5 * 2x) + (5 * -1) - (5x * x) + (5x * 3)

= 6x² - 3x + 10x - 5 - 5x² + 15x

Bước 2: Thu gọn các số hạng đồng dạng

= (6x² - 5x²) + (-3x + 10x + 15x) - 5

= x² + 22x - 5

Bước 3: Kết quả cuối cùng

Vậy, (3x + 5)(2x - 1) - 5x(x - 3) = x² + 22x - 5

Lưu ý quan trọng

Luôn kiểm tra lại các phép tính để tránh sai sót.
Nắm vững các quy tắc về dấu ngoặc và quy tắc chuyển vế.
Thực hành nhiều bài tập tương tự để củng cố kiến thức.

Mở rộng kiến thức

Các bài tập về rút gọn biểu thức đại số là nền tảng quan trọng cho việc học các kiến thức nâng cao hơn trong Toán học. Việc nắm vững các kỹ năng này sẽ giúp học sinh giải quyết các bài toán phức tạp một cách dễ dàng hơn.

Ví dụ tương tự

Để hiểu rõ hơn về cách giải các bài tập tương tự, chúng ta hãy xem xét một ví dụ khác:

(2x - 3)(x + 4) + 3x(2 - x)

Giải:

(2x - 3)(x + 4) + 3x(2 - x) = (2x * x) + (2x * 4) + (-3 * x) + (-3 * 4) + (3x * 2) + (3x * -x)

= 2x² + 8x - 3x - 12 + 6x - 3x²

= (2x² - 3x²) + (8x - 3x + 6x) - 12

= -x² + 11x - 12

Kết luận

Bài 7 trang 67 SGK Toán 8 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bằng cách nắm vững các quy tắc và thực hành nhiều bài tập, học sinh có thể tự tin giải quyết các bài toán tương tự.

Bảng tóm tắt các quy tắc cần nhớ

Quy tắc	Mô tả
Phân phối	a(b + c) = ab + ac
Chuyển vế	Nếu a = b thì a - b = 0
Dấu ngoặc	Chú ý dấu trừ phía trước ngoặc sẽ đổi dấu tất cả các số hạng bên trong ngoặc.