Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 13, 14, 15 sách giáo khoa Toán 8 tập 1 – Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ bản chất của bài học và tự tin giải các bài tập tương tự. Hãy cùng chúng tôi khám phá lời giải ngay sau đây!
Hình hộp chữ nhật (A) có chiều rộng (2x), chiều dài và chiều cao đề gấp (k) lần chiều rộng (Hình 2).
Video hướng dẫn giải
Thực hiện các phép nhân:
a) \(\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right)\)
b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right)\)
Phương pháp giải:
- Để nhân đơn thức với đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức rồi cộng các kết quả với nhau.
- Để nhân hai đa thức, ta nhân từng hạng tử của đa thức này với đa thức kia, rồi cộng các kết quả với nhau
Lời giải chi tiết:
a) \[\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right) = - 5{a^4}.{a^2}b + 5{a^4}.a{b^2} = - 5{a^6}b + 5{a^5}{b^2}\]
b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right) = x.x{y^2} - x.2{y^3} + 2y.x{y^2} - 2y.2{y^3} = {x^2}{y^2} - 2x{y^3} + 2x{y^3} - 4{y^4} = {x^2}{y^2} - 4{y^4}\)
Video hướng dẫn giải
Thực hiện các phép nhân đơn thức sau:
a) \(\left( {4{x^3}} \right).\left( { - 6{x^3}y} \right)\)
b) \(\left( { - 2y} \right).\left( { - 5x{y^2}} \right)\)
c) \({\left( { - 2a} \right)^3}.{\left( {2ab} \right)^2}\)
Phương pháp giải:
Để nhân hai đơn thức, ta nhân các hệ số với nhau, nhân các lũy thừa cùng biến, rồi nhân các kết quả đó với nhau.
Lời giải chi tiết:
a) \(\left( {4{x^3}} \right).\left( { - 6{x^3}y} \right) = \left[ {4.\left( { - 6} \right)} \right].\left( {{x^3}.{x^3}} \right).y = - 24{x^6}y\)
b) \(\left( { - 2y} \right).\left( { - 5x{y^2}} \right) = \left[ {\left( { - 2} \right).\left( { - 5} \right)} \right].x.\left( {y.{y^2}} \right) = 10x{y^3}\)
c) \({\left( { - 2a} \right)^3}.{\left( {2ab} \right)^2} = - 8{a^3}.4{a^2}{b^2} = \left[ {\left( { - 8} \right).4} \right].\left( {{a^3}.{a^2}} \right).{b^2} = - 32{a^5}{b^2}\)
Video hướng dẫn giải
Hình hộp chữ nhật \(A\) có chiều rộng \(2x\), chiều dài và chiều cao đề gấp \(k\) lần chiều rộng (Hình 2).
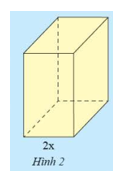
a) Tính diện tích đáy của \(A\).
b) Tính thể tích của \(A\).
Phương pháp giải:
Để nhân hai đơn thức, ta nhận các hệ số với nhau, nhân các lũy thừa cùng biến, rồi nhân các kết quả đó với nhau.
a) Diện tích đáy của hình hộp chữ nhật: \(S = ab\)
b) Thể tích của hình hộp chữ nhật: \(V = abc\)
trong đó \(a\), \(b\), \(c\) là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật.
Lời giải chi tiết:
a) Chiều dài, chiều cao hình hộp chữ nhật \(A\) là: \(2xk\)
Diện tích đáy của hình hộp chữ nhật \(A\) là: \(2xk.2x = 4k{x^4}\)
b) Thể tích của hình hộp chữ nhật \(A\) là: \(2xk.2x.2xk = 8{k^2}{x^3}\)
Video hướng dẫn giải
Tính diện tích phần tô màu trong Hình 4.
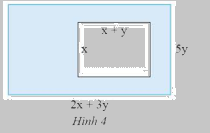
Phương pháp giải:
Áp dụng công thức tính diện tích hình chữ nhật.
Áp dụng qui tắc nhân đa thức, trừ đa thức.
Lời giải chi tiết:
Diện tích hình chữ nhật lớn là: \(5y.\left( {2x + 3y} \right) = 5y.2x + 5y.3y = 10xy + 15{y^2}\)
Diện tích hình chữ nhật nhỏ là: \(x.\left( {x + y} \right) = x.x + x.y = {x^2} + xy\)
Diện tích phần tô màu trong hình 4 là:
\(\left( {10xy + 15{y^2}} \right) - \left( {{x^2} + xy} \right) = 10xy + 15{y^2} - {x^2} - xy = \left( {10xy - xy} \right) + 15{y^2} - {x^2} = 9xy + 15{y^2} - {x^2}\)
Video hướng dẫn giải
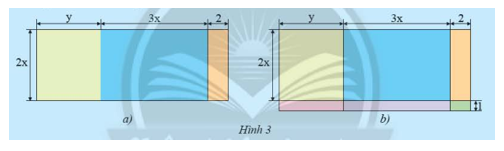
a) Hình 3a là bản vẽ sơ lược sàn của một căn hộ (các kích thước tính theo m). Tính diện tích sàn này bằng những cách khác nhau.
b) Nếu vẽ cả ban công thì được sơ đồ như Hình 3b. Hãy tính tổng diện tích của sàn bao gồm cả ban công.
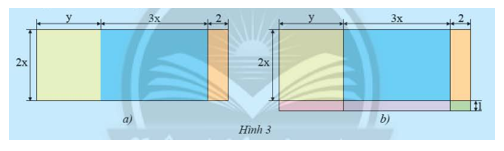
Phương pháp giải:
Sử dụng tính chất phân phối của phép nhân đối với phép cộng, tính chất giao hoán và kết hợp của phép nhân.
Lời giải chi tiết:
a) Cách 1: Diện tích sàn là: \(2x.\left( {y + 3x + 2} \right) = 2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)
Cách 2: Diện tích sàn là: \(2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)
b) Diện tích ban công là: \(1.\left( {y + 3x + 2} \right) = y + 3x + 2\)
Tổng diện tích sàn bao gồm cả ban công là: \(\left( {2xy + 6{x^2} + 4x} \right) + \left( {y + 3x + 2} \right) = 2xy + 6{x^2} + 4x + y + 3x + 2 = 2xy + 6{x^2} + y + 7x + 2\)
Video hướng dẫn giải
Viết biểu thức tính khoảng cách giữa hai phương tiện trong tình hướng ở câu hỏi mở đầu:
Trên một đoạn sông thẳng, xuất phát cùng lúc từ một bến thuyền, thuyền đi xuôi dòng với tốc độ \(\left( {v + 3} \right)\)km/h, ca nô đi ngược dòng với tốc độ \(\left( {2v - 3} \right)\)km/h. Làm thế nào để tìm được quãng đường của mỗi phương tiện và khoảng cách giữa chúng sau khoảng thời gian \(t\) giờ kể từ khi rời bến?

Phương pháp giải:
Quãng đường = vận tốc . thời gian.
Lời giải chi tiết:
Quãng đường thuyền đi xuôi dòng đi được trong khoảng thời gian \(t\) là:
\(\left( {v + 3} \right)t = vt + 3t\) (km)
Quãng đường ca nô đi ngược dòng đi được trong khoảng thời gian \(t\) là:
\(\left( {2v - 3} \right)t = 2vt - 3t\) (km)
Tổng độ dài quãng đường thuyền và ca nô đi được trong khoảng thời gian \(t\) là:
\(\left( {vt + 3t} \right) + \left( {2vt - 3t} \right) = 3vt\) (km)
Gọi khoảng cách lúc đầu giữa hai phương tiện là \(s\) (km).
Khoảng cách giữa hai phương tiện sau khoảng thời gian \(t\) là:
\(s - 3vt\) (km)
Video hướng dẫn giải
Hình hộp chữ nhật \(A\) có chiều rộng \(2x\), chiều dài và chiều cao đề gấp \(k\) lần chiều rộng (Hình 2).
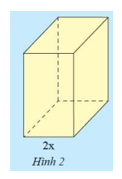
a) Tính diện tích đáy của \(A\).
b) Tính thể tích của \(A\).
Phương pháp giải:
Để nhân hai đơn thức, ta nhận các hệ số với nhau, nhân các lũy thừa cùng biến, rồi nhân các kết quả đó với nhau.
a) Diện tích đáy của hình hộp chữ nhật: \(S = ab\)
b) Thể tích của hình hộp chữ nhật: \(V = abc\)
trong đó \(a\), \(b\), \(c\) là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật.
Lời giải chi tiết:
a) Chiều dài, chiều cao hình hộp chữ nhật \(A\) là: \(2xk\)
Diện tích đáy của hình hộp chữ nhật \(A\) là: \(2xk.2x = 4k{x^4}\)
b) Thể tích của hình hộp chữ nhật \(A\) là: \(2xk.2x.2xk = 8{k^2}{x^3}\)
Video hướng dẫn giải
Thực hiện các phép nhân đơn thức sau:
a) \(\left( {4{x^3}} \right).\left( { - 6{x^3}y} \right)\)
b) \(\left( { - 2y} \right).\left( { - 5x{y^2}} \right)\)
c) \({\left( { - 2a} \right)^3}.{\left( {2ab} \right)^2}\)
Phương pháp giải:
Để nhân hai đơn thức, ta nhân các hệ số với nhau, nhân các lũy thừa cùng biến, rồi nhân các kết quả đó với nhau.
Lời giải chi tiết:
a) \(\left( {4{x^3}} \right).\left( { - 6{x^3}y} \right) = \left[ {4.\left( { - 6} \right)} \right].\left( {{x^3}.{x^3}} \right).y = - 24{x^6}y\)
b) \(\left( { - 2y} \right).\left( { - 5x{y^2}} \right) = \left[ {\left( { - 2} \right).\left( { - 5} \right)} \right].x.\left( {y.{y^2}} \right) = 10x{y^3}\)
c) \({\left( { - 2a} \right)^3}.{\left( {2ab} \right)^2} = - 8{a^3}.4{a^2}{b^2} = \left[ {\left( { - 8} \right).4} \right].\left( {{a^3}.{a^2}} \right).{b^2} = - 32{a^5}{b^2}\)
Video hướng dẫn giải
a) Hình 3a là bản vẽ sơ lược sàn của một căn hộ (các kích thước tính theo m). Tính diện tích sàn này bằng những cách khác nhau.
b) Nếu vẽ cả ban công thì được sơ đồ như Hình 3b. Hãy tính tổng diện tích của sàn bao gồm cả ban công.
Phương pháp giải:
Sử dụng tính chất phân phối của phép nhân đối với phép cộng, tính chất giao hoán và kết hợp của phép nhân.
Lời giải chi tiết:
a) Cách 1: Diện tích sàn là: \(2x.\left( {y + 3x + 2} \right) = 2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)
Cách 2: Diện tích sàn là: \(2x.y + 2x.3x + 2x.2 = 2xy + 6{x^2} + 4x\)
b) Diện tích ban công là: \(1.\left( {y + 3x + 2} \right) = y + 3x + 2\)
Tổng diện tích sàn bao gồm cả ban công là: \(\left( {2xy + 6{x^2} + 4x} \right) + \left( {y + 3x + 2} \right) = 2xy + 6{x^2} + 4x + y + 3x + 2 = 2xy + 6{x^2} + y + 7x + 2\)
Video hướng dẫn giải
Thực hiện các phép nhân:
a) \(\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right)\)
b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right)\)
Phương pháp giải:
- Để nhân đơn thức với đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức rồi cộng các kết quả với nhau.
- Để nhân hai đa thức, ta nhân từng hạng tử của đa thức này với đa thức kia, rồi cộng các kết quả với nhau
Lời giải chi tiết:
a) \[\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right) = - 5{a^4}.{a^2}b + 5{a^4}.a{b^2} = - 5{a^6}b + 5{a^5}{b^2}\]
b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right) = x.x{y^2} - x.2{y^3} + 2y.x{y^2} - 2y.2{y^3} = {x^2}{y^2} - 2x{y^3} + 2x{y^3} - 4{y^4} = {x^2}{y^2} - 4{y^4}\)
Video hướng dẫn giải
Viết biểu thức tính khoảng cách giữa hai phương tiện trong tình hướng ở câu hỏi mở đầu:
Trên một đoạn sông thẳng, xuất phát cùng lúc từ một bến thuyền, thuyền đi xuôi dòng với tốc độ \(\left( {v + 3} \right)\)km/h, ca nô đi ngược dòng với tốc độ \(\left( {2v - 3} \right)\)km/h. Làm thế nào để tìm được quãng đường của mỗi phương tiện và khoảng cách giữa chúng sau khoảng thời gian \(t\) giờ kể từ khi rời bến?

Phương pháp giải:
Quãng đường = vận tốc . thời gian.
Lời giải chi tiết:
Quãng đường thuyền đi xuôi dòng đi được trong khoảng thời gian \(t\) là:
\(\left( {v + 3} \right)t = vt + 3t\) (km)
Quãng đường ca nô đi ngược dòng đi được trong khoảng thời gian \(t\) là:
\(\left( {2v - 3} \right)t = 2vt - 3t\) (km)
Tổng độ dài quãng đường thuyền và ca nô đi được trong khoảng thời gian \(t\) là:
\(\left( {vt + 3t} \right) + \left( {2vt - 3t} \right) = 3vt\) (km)
Gọi khoảng cách lúc đầu giữa hai phương tiện là \(s\) (km).
Khoảng cách giữa hai phương tiện sau khoảng thời gian \(t\) là:
\(s - 3vt\) (km)
Video hướng dẫn giải
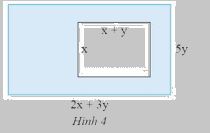
Tính diện tích phần tô màu trong Hình 4.
Phương pháp giải:
Áp dụng công thức tính diện tích hình chữ nhật.
Áp dụng qui tắc nhân đa thức, trừ đa thức.
Lời giải chi tiết:
Diện tích hình chữ nhật lớn là: \(5y.\left( {2x + 3y} \right) = 5y.2x + 5y.3y = 10xy + 15{y^2}\)
Diện tích hình chữ nhật nhỏ là: \(x.\left( {x + y} \right) = x.x + x.y = {x^2} + xy\)
Diện tích phần tô màu trong hình 4 là:
\(\left( {10xy + 15{y^2}} \right) - \left( {{x^2} + xy} \right) = 10xy + 15{y^2} - {x^2} - xy = \left( {10xy - xy} \right) + 15{y^2} - {x^2} = 9xy + 15{y^2} - {x^2}\)
Mục 2 của chương trình Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán với đa thức. Các em sẽ được củng cố các quy tắc cộng, trừ, nhân, chia đa thức, đồng thời làm quen với các bài tập ứng dụng thực tế. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập trong mục 2 trang 13, 14, 15 SGK Toán 8 tập 1 – Chân trời sáng tạo bao gồm các dạng bài tập sau:
Để cộng hoặc trừ các đa thức, các em cần thực hiện các bước sau:
Ví dụ: Tính (2x2 + 3x - 1) + (x2 - 2x + 3)
Giải:
(2x2 + 3x - 1) + (x2 - 2x + 3) = 2x2 + 3x - 1 + x2 - 2x + 3 = (2x2 + x2) + (3x - 2x) + (-1 + 3) = 3x2 + x + 2
Để nhân các đa thức, các em cần áp dụng quy tắc phân phối. Để chia các đa thức, các em có thể sử dụng phương pháp chia đa thức một biến.
Ví dụ: Tính (x + 2)(x - 3)
Giải:
(x + 2)(x - 3) = x(x - 3) + 2(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6
Để rút gọn biểu thức chứa đa thức, các em cần thực hiện các phép toán cộng, trừ, nhân, chia đa thức và kết hợp các hạng tử đồng dạng.
Để tìm giá trị của biểu thức tại một giá trị cụ thể của biến, các em cần thay giá trị của biến vào biểu thức và thực hiện các phép tính.
Các bài toán ứng dụng thực tế thường yêu cầu các em sử dụng các phép toán với đa thức để mô tả và giải quyết các vấn đề trong cuộc sống.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải các bài tập mục 2 trang 13, 14, 15 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!