Bài 4 trang 57 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 57 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác
Đề bài
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm,AC = 4cm.\) Đường phân giác của góc \(A\) cắt \(BC\) tại \(D\).
a) Tính \(BC,BD,DC\).
b) Vẽ đường cao \(AH\). Tính \(AH,HD\) và \(AD\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Sử dụng Tính chất đường phân giác trong tam giác:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
- Định lí Py – ta – go
Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết
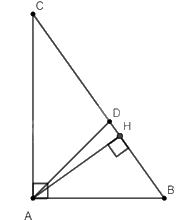
a) Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( {3^2} + {4^2} = B{C^2}\)
\( B{C^2} = 25\)
Suy ra \( BC = 5cm\)
Ta có: \(BD + DC = BC \) suy ra \(DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\)
\(\frac{{BD}}{{5 - BD}} = \frac{3}{4} \)
\(4.BD = 3.\left( {5 - BD} \right)\)
suy ra \( 4.BD = 15 - 3.BD\)
\( 4BD + 3BD = 15\)
\(7BD = 15\) nên \(BD = \frac{{15}}{7}\)
Suy ra \(DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
Suy ra \( AH = \frac{{6.2}}{5} = \frac{{12}}{5}cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( H{B^2} = A{B^2} - A{H^2}\)
\( H{B^2} = {3^2} - \left( \frac{{12}}{5} \right)^2\)
\( H{B^2} = \frac{{81}}{25}\)
Suy ra \(HB = \frac{{9}}{5}cm\)
\(HD = BD - BH = \frac{{15}}{7} - \frac{{9}}{5} = \frac{{12}}{35}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( A{D^2} = \left( \frac{{12}}{35} \right)^2 + \left( \frac{{12}}{5} \right)^2\)
\( A{D^2} = \frac{{144}}{{1225}} + \frac{{144}}{{25}}\)
\( A{D^2} = \frac{{288}}{{49}}\)
Suy ra \(AD = \frac{{12\sqrt 2}}{{7}} cm\)
Vậy \(AH = \frac{{12}}{{5}}cm;HD = \frac{{12}}{35}cm;AD = \frac{{12\sqrt 2}}{{7}}cm\).
Bài 4 trang 57 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh thực hiện các phép biến đổi đại số để rút gọn biểu thức hoặc giải phương trình. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài tập. Giả sử bài tập yêu cầu rút gọn biểu thức sau:
(x + 2)(x - 2) + (x + 1)^2
Lời giải:
Vậy, (x + 2)(x - 2) + (x + 1)^2 = 2x^2 + 2x - 3
Ngoài bài 4 trang 57, SGK Toán 8 tập 2 – Chân trời sáng tạo còn có nhiều bài tập tương tự yêu cầu học sinh vận dụng các kiến thức về phép biến đổi đại số. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập này, học sinh cần:
Kiến thức về phép biến đổi đại số không chỉ quan trọng trong môn Toán mà còn có ứng dụng rộng rãi trong các lĩnh vực khác như Vật lý, Hóa học, Kinh tế. Việc nắm vững kiến thức này sẽ giúp học sinh giải quyết các bài toán thực tế một cách hiệu quả hơn.
Để củng cố kiến thức, các em học sinh có thể tự giải các bài tập sau:
Bài 4 trang 57 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về phép biến đổi đại số. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn Toán.