Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 69, 70 SGK Toán 8 tập 2 – Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập trong mục này tập trung vào các kiến thức quan trọng của chương trình Toán 8, đòi hỏi các em phải vận dụng linh hoạt các công thức và định lý đã học.
Cho hai tam giác
Video hướng dẫn giải
Qua các trường hợp đồng dạng của hai tam giác, hãy trả lời câu hỏi ở đầu bài (trang 67).
Phương pháp giải:
Dựa vào cách chứng minh hai tam giác bằng nhau và hai tam giác đồng dạng.
Lời giải chi tiết:
- Ở hai tam giác bằng nhau yêu cầu các cạnh tương ứng bằng nhau còn ở hai tam giác đồng dạng yêu cầu các cạnh tương ứng có cùng tỉ lê.
- Hai tam giác bằng nhau có ba trường hợp: cạnh góc cạnh, cạnh cạnh cạnh, góc cạnh góc.
- Hai tam giác đồng dạng có ba trường hợp: cạnh góc cạnh, cạnh cạnh cạnh, góc góc.
Video hướng dẫn giải
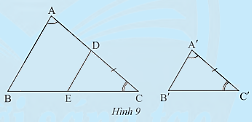
Cho hai tam giác \(ABC\) và \(A'B'C'\) có \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\) (Hình 9).
Trên cạnh \(AC\), lấy điểm \(D\) sao cho \(DC = A'C'\). Qua \(D\) là kẻ đường thẳng song song với \(AB\) cắt cạnh \(BC\) tại \(E\).
a) Tam giác \(DEC\) có đồng dạng với tam giác \(ABC\) không?
b) Nhận xét về mối quan hệ giữa tam giác \(A'B'C'\)và tam giác \(DEC\).
c) Dự đoán về sự đồng dạng của hai tam giác \(A'B'C'\)và \(ABC\).
Phương pháp giải:
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
- Hai tam giác bằng nhau thì đồng dạng với nhau.
Lời giải chi tiết:
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).
Video hướng dẫn giải
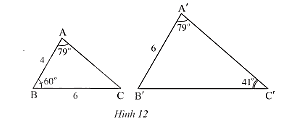
Quan sát Hình 12.
a) Chứng minh \(\Delta ABC\backsim\Delta A'B'C'\).
b) Tính độ dài cạnh \(B'C'\).
Phương pháp giải:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Tổng ba góc trong một tam giác có số đo bằng \(180^\circ \).
Lời giải chi tiết:
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).
Video hướng dẫn giải
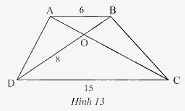
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có \(AB = 6m,CD = 15m,OD = 8m\) (Hình 13). Tính độ dài đoạn thẳng \(OB\).
Phương pháp giải:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Vì tứ giác \(ABCD\) là hình thang có \(AB//CD\) nên \(\widehat {BAO} = \widehat {OCD}\) (hai góc so le trong)
Xét tam giác \(ABO\) và tam giác \(CDO\) có:
\(\widehat {BAO} = \widehat {OCD}\) (chứng minh trên)
\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
Do đó, \(\Delta ABO\backsim\Delta CDO\) (g.g)
Ta có: \(\frac{{AB}}{{CD}} = \frac{{OB}}{{OD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{6}{{15}} = \frac{{OB}}{8} \Rightarrow OB = \frac{{6.8}}{{15}} = 3,2\)
Vậy \(OB = 3,2m\).
Video hướng dẫn giải
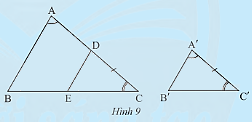
Cho hai tam giác \(ABC\) và \(A'B'C'\) có \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\) (Hình 9).
Trên cạnh \(AC\), lấy điểm \(D\) sao cho \(DC = A'C'\). Qua \(D\) là kẻ đường thẳng song song với \(AB\) cắt cạnh \(BC\) tại \(E\).
a) Tam giác \(DEC\) có đồng dạng với tam giác \(ABC\) không?
b) Nhận xét về mối quan hệ giữa tam giác \(A'B'C'\)và tam giác \(DEC\).
c) Dự đoán về sự đồng dạng của hai tam giác \(A'B'C'\)và \(ABC\).
Phương pháp giải:
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
- Hai tam giác bằng nhau thì đồng dạng với nhau.
Lời giải chi tiết:
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).
Video hướng dẫn giải
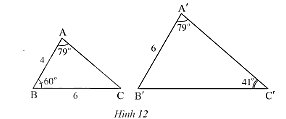
Quan sát Hình 12.
a) Chứng minh \(\Delta ABC\backsim\Delta A'B'C'\).
b) Tính độ dài cạnh \(B'C'\).
Phương pháp giải:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Tổng ba góc trong một tam giác có số đo bằng \(180^\circ \).
Lời giải chi tiết:
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).
Video hướng dẫn giải
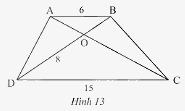
Cho hình thang \(ABCD\left( {AB//CD} \right)\) có \(AB = 6m,CD = 15m,OD = 8m\) (Hình 13). Tính độ dài đoạn thẳng \(OB\).
Phương pháp giải:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Vì tứ giác \(ABCD\) là hình thang có \(AB//CD\) nên \(\widehat {BAO} = \widehat {OCD}\) (hai góc so le trong)
Xét tam giác \(ABO\) và tam giác \(CDO\) có:
\(\widehat {BAO} = \widehat {OCD}\) (chứng minh trên)
\(\widehat {AOB} = \widehat {COD}\) (hai góc đối đỉnh)
Do đó, \(\Delta ABO\backsim\Delta CDO\) (g.g)
Ta có: \(\frac{{AB}}{{CD}} = \frac{{OB}}{{OD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{6}{{15}} = \frac{{OB}}{8} \Rightarrow OB = \frac{{6.8}}{{15}} = 3,2\)
Vậy \(OB = 3,2m\).
Video hướng dẫn giải
Qua các trường hợp đồng dạng của hai tam giác, hãy trả lời câu hỏi ở đầu bài (trang 67).
Phương pháp giải:
Dựa vào cách chứng minh hai tam giác bằng nhau và hai tam giác đồng dạng.
Lời giải chi tiết:
- Ở hai tam giác bằng nhau yêu cầu các cạnh tương ứng bằng nhau còn ở hai tam giác đồng dạng yêu cầu các cạnh tương ứng có cùng tỉ lê.
- Hai tam giác bằng nhau có ba trường hợp: cạnh góc cạnh, cạnh cạnh cạnh, góc cạnh góc.
- Hai tam giác đồng dạng có ba trường hợp: cạnh góc cạnh, cạnh cạnh cạnh, góc góc.
Mục 3 trang 69, 70 SGK Toán 8 tập 2 – Chân trời sáng tạo là một phần quan trọng trong chương trình học, tập trung vào việc củng cố và mở rộng kiến thức về các dạng bài tập liên quan đến hình học, đặc biệt là các bài toán về tứ giác. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững các định nghĩa, tính chất và định lý liên quan đến tứ giác, đồng thời rèn luyện kỹ năng phân tích đề bài và lựa chọn phương pháp giải phù hợp.
Mục 3 bao gồm các bài tập vận dụng các kiến thức đã học về:
Bài 1 yêu cầu học sinh chứng minh một tứ giác là hình bình hành. Để giải bài này, học sinh cần vận dụng các dấu hiệu nhận biết hình bình hành:
Ví dụ, nếu đề bài cho tứ giác ABCD có AB song song CD và AD song song BC, thì ABCD là hình bình hành.
Bài 2 thường liên quan đến việc tính toán các yếu tố của hình bình hành, hình chữ nhật, hình thoi hoặc hình vuông. Học sinh cần sử dụng các công thức tính diện tích, chu vi, độ dài đường chéo, góc của các hình này.
Ví dụ, để tính diện tích hình chữ nhật, ta sử dụng công thức: Diện tích = chiều dài x chiều rộng.
Bài 3 có thể là một bài toán ứng dụng thực tế, yêu cầu học sinh vận dụng kiến thức về tứ giác để giải quyết các vấn đề liên quan đến cuộc sống hàng ngày.
Ví dụ, một bài toán có thể yêu cầu tính chiều dài của một đoạn dây cần thiết để căng một tấm bạt hình chữ nhật.
Để giải các bài tập trong Mục 3 một cách hiệu quả, học sinh nên:
Khi giải các bài tập về tứ giác, học sinh cần chú ý đến các tính chất và định lý liên quan. Đồng thời, cần rèn luyện kỹ năng vẽ hình và phân tích đề bài để có thể giải quyết các bài toán một cách nhanh chóng và chính xác.
Giải mục 3 trang 69, 70 SGK Toán 8 tập 2 – Chân trời sáng tạo đòi hỏi sự nắm vững kiến thức và kỹ năng vận dụng linh hoạt. Hy vọng với hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em học sinh sẽ tự tin giải quyết các bài tập và đạt kết quả tốt trong môn Toán.
| Hình dạng | Công thức tính diện tích |
|---|---|
| Hình chữ nhật | Chiều dài x Chiều rộng |
| Hình thoi | (Đường chéo 1 x Đường chéo 2) / 2 |
| Hình bình hành | Chiều dài x Chiều cao |
| Bảng tổng hợp công thức tính diện tích các hình tứ giác | |