Bài 1 trang 58 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh thực hiện các phép tính, rút gọn biểu thức hoặc chứng minh đẳng thức.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1 trang 58 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác
Đề bài
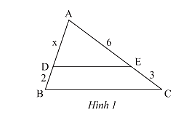
Cho tam giác \(ABC\), biết \(DE//BC\) và \(AE = 6cm,EC = 3cm,DB = 2cm\) (Hình 1). Độ dài đoạn thẳng \(AD\) là
A. 4cm.
B. 3 cm.
C. 5cm.
D. 3,5 cm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
Chọn đáp án A
Xét tam giác \(ABC\) có \(DE//BC\) nên theo định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow \frac{x}{2} = \frac{6}{3}\). Do đó, \(x = \frac{{6.2}}{3} = 4\).
Vậy \(x = 4\).
Bài 1 trang 58 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số đã học để giải quyết các bài toán cụ thể. Để giải bài tập này hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như đơn thức, đa thức, các phép cộng, trừ, nhân, chia đơn thức, đa thức, và các hằng đẳng thức đáng nhớ.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 1:
Giả sử biểu thức cần rút gọn là: 3x2 + 2x - 5x2 + 7x - 1
Lời giải:
Giả sử biểu thức đã rút gọn ở phần a là: -2x2 + 9x - 1 và x = 2
Lời giải:
Giả sử đẳng thức cần chứng minh là: (a + b)2 = a2 + 2ab + b2
Lời giải:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong SGK Toán 8 tập 2 – Chân trời sáng tạo hoặc các đề thi thử Toán 8.
Bài 1 trang 58 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.