Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 10, 11 SGK Toán 8 tập 1 Chân trời sáng tạo trên giaitoan.edu.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn bộ giải bài tập Toán 8 tập 1 Chân trời sáng tạo đầy đủ và chính xác, giúp các em nắm vững kiến thức và tự tin giải quyết mọi bài toán.
Cho hai đa thức (A = 5{x^2} - 4xy + 2x - 4{x^2} + xy); (B = {x^2} - 3xy + 2x). Tính giá trị của (A) và (B) tại (x = - 2); (y = dfrac{1}{3}). So sánh hai kết quả nhận được.
Video hướng dẫn giải
Cho hai đa thức \(A = 5{x^2} - 4xy + 2x - 4{x^2} + xy\); \(B = {x^2} - 3xy + 2x\).
Tính giá trị của \(A\) và \(B\) tại \(x = - 2\); \(y = \dfrac{1}{3}\). So sánh hai kết quả nhận được.
Phương pháp giải:
Tính giá trị các đa thức \(A\), \(B\) khi \(x = - 2\); \(y = \dfrac{1}{3}\).
So sánh hai kết quả nhận được.
Lời giải chi tiết:
Thay \(x = - 2\); \(y = \dfrac{1}{3}\) vào đa thức \(A\) ta có:
\(\begin{array}{l}A = 5.{\left( { - 2} \right)^2} - 4.\left( { - 2} \right).\dfrac{1}{3} + 2.\left( { - 2} \right) - 4.{\left( { - 2} \right)^2} + \left( { - 2} \right).\dfrac{1}{3}\\A = 5.4 - \dfrac{{ - 8}}{3} + \left( { - 4} \right) - 4.4 + \dfrac{{ - 2}}{3}\\A = 20 + \dfrac{8}{3} - 4 - 16 + \dfrac{{ - 2}}{3}\\A = 2\end{array}\)
Thay \(x = - 2\); \(y = \dfrac{1}{3}\) vào đa thức \(B\) ta có:
\(\begin{array}{l}B = {\left( { - 2} \right)^2} - 3.\left( { - 2} \right).\dfrac{1}{3} + 2.\left( { - 2} \right)\\B = 4 - \left( { - 2} \right) + \left( { - 4} \right)\\B = 4 + 2 - 4\\B = 2\end{array}\)
Vậy \(A = B\)
Video hướng dẫn giải
Tính giá trị của đa thức \(A = 3{x^2}y - 5xy - 2{x^2}y - 3xy\) tại \(x = 3\); \(y = - \dfrac{1}{2}\).
Phương pháp giải:
- Thu gọn đa thức
- Tính giá trị của đa thức thu gọn khi \(x = 3\); \(y = - \dfrac{1}{2}\).
Lời giải chi tiết:
Ta có:
\(A = 3{x^2}y - 5xy - 2{x^2}y - 3xy = \left( {3{x^2}y - 2{x^2}y} \right) + \left( { - 5xy - 3xy} \right) = {x^2}y - 8xy\)
Thay \(x = 3\); \(y = - \dfrac{1}{2}\) vào đa thức \(A\) ta có:
\(A = {3^2}.\left( { - \dfrac{1}{2}} \right) - 8.3.\left( { - \dfrac{1}{2}} \right) = \dfrac{{ - 9}}{2} - \left( { - 12} \right) = \dfrac{{15}}{2}\)
Vậy \(A = \dfrac{{15}}{2}\) khi \(x = 3\); \(y = - \dfrac{1}{2}\).
Video hướng dẫn giải
Thu gọn và tìm bậc của mỗi đa thức sau:
a) \(A = x - 2y + xy - 3x + {y^2}\)
b) \(B = xyz - {x^2}y + xz - \dfrac{1}{2}xyz + \dfrac{1}{2}xz\)
Phương pháp giải:
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng với nhau.
Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.
Lời giải chi tiết:
a) Ta có:
\(A = x - 2y + xy - 3x + {y^2} = \left( {x - 3x} \right) - 2y + xy + {y^2} = - 2x - 2y + xy + {y^2}\)
Bốn hạng tử của \(A\) lần lượt có bậc là \(1\), \(1\), \(2\), \(2\). Do đó bậc của đa thức \(A\) là \(2\).
b) Ta có:
\(B = xyz - {x^2}y + xz - \dfrac{1}{2}xyz + \dfrac{1}{2}xz = \left( {xyz - \dfrac{1}{2}xyz} \right) - {x^2}y + \left( {xz + \dfrac{1}{2}xz} \right) = \dfrac{1}{2}xyz - {x^2}y + \dfrac{3}{2}xz\)
Ba hạng tử của \(B\) lần lượt có bậc là \(3\), \(3\), \(2\). Do đó bậc của đa thức \(B\) là \(3\).
Video hướng dẫn giải
Cho hai đa thức \(A = 5{x^2} - 4xy + 2x - 4{x^2} + xy\); \(B = {x^2} - 3xy + 2x\).
Tính giá trị của \(A\) và \(B\) tại \(x = - 2\); \(y = \dfrac{1}{3}\). So sánh hai kết quả nhận được.
Phương pháp giải:
Tính giá trị các đa thức \(A\), \(B\) khi \(x = - 2\); \(y = \dfrac{1}{3}\).
So sánh hai kết quả nhận được.
Lời giải chi tiết:
Thay \(x = - 2\); \(y = \dfrac{1}{3}\) vào đa thức \(A\) ta có:
\(\begin{array}{l}A = 5.{\left( { - 2} \right)^2} - 4.\left( { - 2} \right).\dfrac{1}{3} + 2.\left( { - 2} \right) - 4.{\left( { - 2} \right)^2} + \left( { - 2} \right).\dfrac{1}{3}\\A = 5.4 - \dfrac{{ - 8}}{3} + \left( { - 4} \right) - 4.4 + \dfrac{{ - 2}}{3}\\A = 20 + \dfrac{8}{3} - 4 - 16 + \dfrac{{ - 2}}{3}\\A = 2\end{array}\)
Thay \(x = - 2\); \(y = \dfrac{1}{3}\) vào đa thức \(B\) ta có:
\(\begin{array}{l}B = {\left( { - 2} \right)^2} - 3.\left( { - 2} \right).\dfrac{1}{3} + 2.\left( { - 2} \right)\\B = 4 - \left( { - 2} \right) + \left( { - 4} \right)\\B = 4 + 2 - 4\\B = 2\end{array}\)
Vậy \(A = B\)
Video hướng dẫn giải
Thu gọn và tìm bậc của mỗi đa thức sau:
a) \(A = x - 2y + xy - 3x + {y^2}\)
b) \(B = xyz - {x^2}y + xz - \dfrac{1}{2}xyz + \dfrac{1}{2}xz\)
Phương pháp giải:
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng với nhau.
Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.
Lời giải chi tiết:
a) Ta có:
\(A = x - 2y + xy - 3x + {y^2} = \left( {x - 3x} \right) - 2y + xy + {y^2} = - 2x - 2y + xy + {y^2}\)
Bốn hạng tử của \(A\) lần lượt có bậc là \(1\), \(1\), \(2\), \(2\). Do đó bậc của đa thức \(A\) là \(2\).
b) Ta có:
\(B = xyz - {x^2}y + xz - \dfrac{1}{2}xyz + \dfrac{1}{2}xz = \left( {xyz - \dfrac{1}{2}xyz} \right) - {x^2}y + \left( {xz + \dfrac{1}{2}xz} \right) = \dfrac{1}{2}xyz - {x^2}y + \dfrac{3}{2}xz\)
Ba hạng tử của \(B\) lần lượt có bậc là \(3\), \(3\), \(2\). Do đó bậc của đa thức \(B\) là \(3\).
Video hướng dẫn giải
Tính giá trị của đa thức \(A = 3{x^2}y - 5xy - 2{x^2}y - 3xy\) tại \(x = 3\); \(y = - \dfrac{1}{2}\).
Phương pháp giải:
- Thu gọn đa thức
- Tính giá trị của đa thức thu gọn khi \(x = 3\); \(y = - \dfrac{1}{2}\).
Lời giải chi tiết:
Ta có:
\(A = 3{x^2}y - 5xy - 2{x^2}y - 3xy = \left( {3{x^2}y - 2{x^2}y} \right) + \left( { - 5xy - 3xy} \right) = {x^2}y - 8xy\)
Thay \(x = 3\); \(y = - \dfrac{1}{2}\) vào đa thức \(A\) ta có:
\(A = {3^2}.\left( { - \dfrac{1}{2}} \right) - 8.3.\left( { - \dfrac{1}{2}} \right) = \dfrac{{ - 9}}{2} - \left( { - 12} \right) = \dfrac{{15}}{2}\)
Vậy \(A = \dfrac{{15}}{2}\) khi \(x = 3\); \(y = - \dfrac{1}{2}\).
Video hướng dẫn giải
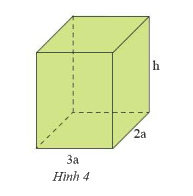
Cho hình hộp chữ nhật có các kịch thước như hình 4 (tính theo cm).
a) Viết các biểu thức tính thể tích và diện tích xung quang của hình hộp chữ nhật đó.
b) Tính giá trị của các đại lượng trên khi \(a = 2\)cm; \(h = 5\)cm.
Phương pháp giải:
a) Công thức tính thể tích và diện tích xung quanh của hình hộp chữ nhật:
\(V = a.b.h\)
\({S_{xq}} = \left( {a + b} \right).2.h\)
Trong đó \(V\), \({S_{xq}}\), \(a\), \(b\), \(h\) lần lượt là thể tích, diện tích xung quanh, chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật.
b) Tính giá trị biểu thức \(V\), \({S_{xq}}\) khi \(a = 2\)cm; \(h = 5\)cm.
Lời giải chi tiết:
a) Biểu thức tính thể tích của hình hộp chữ nhật: \(V = 3a.2a.h = 6{a^2}h\)
Biểu thức tính diện tích xung quanh của hình hộp chữ nhật: \({S_{xq}} = \left( {3a + 2a} \right).2.h = 5a.2.h = 10ah\)
b) Thay \(a = 2\)cm; \(h = 5\)cm vào các biểu thức trên ta có:
\(V = {6.2^2}.5 = 6.4.5 = 120\) (\(c{m^3}\))
\({S_{xq}} = 10.2.5 = 100\) (\(c{m^2}\))
Video hướng dẫn giải
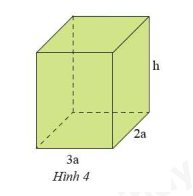
Cho hình hộp chữ nhật có các kịch thước như hình 4 (tính theo cm).
a) Viết các biểu thức tính thể tích và diện tích xung quang của hình hộp chữ nhật đó.
b) Tính giá trị của các đại lượng trên khi \(a = 2\)cm; \(h = 5\)cm.
Phương pháp giải:
a) Công thức tính thể tích và diện tích xung quanh của hình hộp chữ nhật:
\(V = a.b.h\)
\({S_{xq}} = \left( {a + b} \right).2.h\)
Trong đó \(V\), \({S_{xq}}\), \(a\), \(b\), \(h\) lần lượt là thể tích, diện tích xung quanh, chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật.
b) Tính giá trị biểu thức \(V\), \({S_{xq}}\) khi \(a = 2\)cm; \(h = 5\)cm.
Lời giải chi tiết:
a) Biểu thức tính thể tích của hình hộp chữ nhật: \(V = 3a.2a.h = 6{a^2}h\)
Biểu thức tính diện tích xung quanh của hình hộp chữ nhật: \({S_{xq}} = \left( {3a + 2a} \right).2.h = 5a.2.h = 10ah\)
b) Thay \(a = 2\)cm; \(h = 5\)cm vào các biểu thức trên ta có:
\(V = {6.2^2}.5 = 6.4.5 = 120\) (\(c{m^3}\))
\({S_{xq}} = 10.2.5 = 100\) (\(c{m^2}\))
Mục 4 trong SGK Toán 8 tập 1 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về phép nhân đa thức, hằng đẳng thức đáng nhớ và ứng dụng của chúng trong giải toán. Đây là một phần quan trọng, đặt nền móng cho các kiến thức nâng cao hơn trong chương trình học. Việc nắm vững các khái niệm và kỹ năng trong mục này sẽ giúp học sinh tự tin hơn khi đối mặt với các bài toán phức tạp.
Mục 4 bao gồm các bài tập rèn luyện kỹ năng nhân đa thức, sử dụng các hằng đẳng thức để biến đổi biểu thức và giải các bài toán thực tế. Các bài tập được chia thành nhiều mức độ khác nhau, từ dễ đến khó, giúp học sinh có thể tự đánh giá năng lực và cải thiện kỹ năng của mình.
Bài 1 tập trung vào việc thực hành các phép nhân đa thức. Học sinh cần nắm vững quy tắc nhân đơn thức với đa thức, đa thức với đa thức và áp dụng các quy tắc này để tính toán chính xác.
Bài 2 yêu cầu học sinh vận dụng các hằng đẳng thức đáng nhớ để biến đổi biểu thức và giải toán. Các hằng đẳng thức thường được sử dụng bao gồm:
Ví dụ 2: Tính (x + 2)2
Giải: (x + 2)2 = x2 + 2 * x * 2 + 22 = x2 + 4x + 4
Bài 3 là phần ứng dụng, yêu cầu học sinh sử dụng kiến thức đã học để giải các bài toán thực tế. Các bài toán này thường liên quan đến việc tính diện tích, chu vi, hoặc các đại lượng khác trong hình học.
Giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập trong mục 4 trang 10, 11 SGK Toán 8 tập 1 Chân trời sáng tạo. Các lời giải được trình bày rõ ràng, dễ hiểu, kèm theo các bước giải cụ thể và giải thích chi tiết. Học sinh có thể tham khảo để hiểu rõ phương pháp giải và tự giải các bài tập tương tự.
Ngoài SGK Toán 8 tập 1 Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức:
Việc giải bài tập mục 4 trang 10, 11 SGK Toán 8 tập 1 Chân trời sáng tạo là một bước quan trọng trong quá trình học Toán 8. Hy vọng rằng với sự hỗ trợ của giaitoan.edu.vn, các em sẽ tự tin hơn và đạt kết quả tốt trong môn học này.