Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải quyết hoàn toàn mục 3 trang 25 SGK Toán 8 tập 1 – Chân trời sáng tạo, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và dễ tiếp cận, hỗ trợ tối đa cho quá trình học tập của bạn.
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử: ({a^2} + ab + 2a + 2b = left( {{a^2} + ab} right) + left( {2a + 2b} right) = ...) Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
Video hướng dẫn giải
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
\({a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...\)
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
\({a^2} + ab + 2a + 2b \\= \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) \\= a\left( {a + b} \right) + 2\left( {a + b} \right) \\= \left( {a + b} \right)\left( {a + 2} \right)\)
Cách khác:
\({a^2} + ab + 2a + 2b \\= \left( {{a^2} + 2a} \right) + \left( {ab + 2b} \right) \\= a\left( {a + 2} \right) + b\left( {a + 2} \right) \\= \left( {a + 2} \right)\left( {a + b} \right)\)
Video hướng dẫn giải
Phân tích các đa thức sau thành nhân tử:
a) \({a^3} - {a^2}b + a - b\)
b) \({x^2} - {y^2} + 2y - 1\)
Phương pháp giải:
a) Sử dụng phương pháp nhóm hạng tử
b) Sử dụng phương pháp nhóm hạng tử, hẳng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\), \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
Lời giải chi tiết:
a) \({a^3} - {a^2}b + a - b\)
\( = \left( {{a^3} - {a^2}b} \right) + \left( {a - b} \right) \\= {a^2}\left( {a - b} \right) + \left( {a - b} \right) \\= \left( {a - b} \right)\left( {{a^2} + 1} \right)\)
b) \({x^2} - {y^2} + 2y - 1\)
\( = {x^2} - {\left( {{y^2} - 2y + 1} \right)^2} = {x^2} - {\left( {y - 1} \right)^2} \\= \left[ {x + \left( {y - 1} \right)} \right]\left[ {x - \left( {y - 1} \right)} \right] \\= \left( {x + y - 1} \right)\left( {x - y + 1} \right)\)
Video hướng dẫn giải
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
\({a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...\)
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
\({a^2} + ab + 2a + 2b \\= \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) \\= a\left( {a + b} \right) + 2\left( {a + b} \right) \\= \left( {a + b} \right)\left( {a + 2} \right)\)
Cách khác:
\({a^2} + ab + 2a + 2b \\= \left( {{a^2} + 2a} \right) + \left( {ab + 2b} \right) \\= a\left( {a + 2} \right) + b\left( {a + 2} \right) \\= \left( {a + 2} \right)\left( {a + b} \right)\)
Video hướng dẫn giải
Phân tích các đa thức sau thành nhân tử:
a) \({a^3} - {a^2}b + a - b\)
b) \({x^2} - {y^2} + 2y - 1\)
Phương pháp giải:
a) Sử dụng phương pháp nhóm hạng tử
b) Sử dụng phương pháp nhóm hạng tử, hẳng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\), \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
Lời giải chi tiết:
a) \({a^3} - {a^2}b + a - b\)
\( = \left( {{a^3} - {a^2}b} \right) + \left( {a - b} \right) \\= {a^2}\left( {a - b} \right) + \left( {a - b} \right) \\= \left( {a - b} \right)\left( {{a^2} + 1} \right)\)
b) \({x^2} - {y^2} + 2y - 1\)
\( = {x^2} - {\left( {{y^2} - 2y + 1} \right)^2} = {x^2} - {\left( {y - 1} \right)^2} \\= \left[ {x + \left( {y - 1} \right)} \right]\left[ {x - \left( {y - 1} \right)} \right] \\= \left( {x + y - 1} \right)\left( {x - y + 1} \right)\)
Video hướng dẫn giải
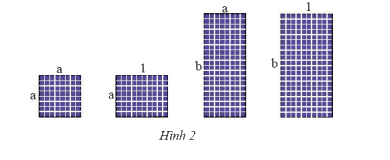
Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết \(a = 0,8\); \(b = 2\) (các kích thước tính theo mét).
Phương pháp giải:
Diện tích hình chữ nhật = chiều dài . chiều rộng
Lời giải chi tiết:
Có thể ghép bốn tấm thành một hình chữ nhật.
Khi đó, chiều dài hình chữ nhật là: \(a + b = 0,8 + 2 = 2,8\)
Khi đó, chiều rộng hình chữ nhật là: \(a + 1 = 0,8 + 1 = 1,8\)
Diện tích hình chữ nhật là: \(2,8.1,8 = 5,04\)
Video hướng dẫn giải
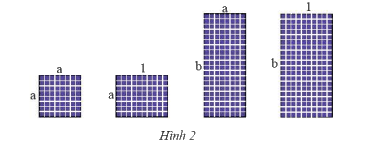
Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết \(a = 0,8\); \(b = 2\) (các kích thước tính theo mét).
Phương pháp giải:
Diện tích hình chữ nhật = chiều dài . chiều rộng
Lời giải chi tiết:
Có thể ghép bốn tấm thành một hình chữ nhật.
Khi đó, chiều dài hình chữ nhật là: \(a + b = 0,8 + 2 = 2,8\)
Khi đó, chiều rộng hình chữ nhật là: \(a + 1 = 0,8 + 1 = 1,8\)
Diện tích hình chữ nhật là: \(2,8.1,8 = 5,04\)
Mục 3 trang 25 SGK Toán 8 tập 1 – Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến các phép biến đổi đại số đơn giản, các biểu thức đại số và việc rút gọn biểu thức. Để giải quyết các bài toán này, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất của phép cộng, trừ, nhân, chia và các quy tắc về dấu ngoặc.
Mục 3 thường bao gồm một số bài tập nhỏ, mỗi bài tập yêu cầu học sinh áp dụng một hoặc nhiều kiến thức đã học để tìm ra kết quả. Các bài tập có thể được trình bày dưới dạng:
Để giúp bạn hiểu rõ hơn về cách giải các bài tập trong Mục 3 trang 25, chúng tôi sẽ cung cấp hướng dẫn chi tiết cho từng bài tập. Dưới đây là ví dụ về cách giải một bài tập thường gặp:
Để đạt được kết quả tốt nhất khi giải các bài tập trong Mục 3 trang 25, bạn cần lưu ý những điều sau:
Ngoài việc giải các bài tập trong SGK, bạn có thể tìm hiểu thêm về các kiến thức liên quan đến đại số thông qua các nguồn tài liệu khác như sách tham khảo, các trang web học toán online, hoặc các video hướng dẫn. Việc mở rộng kiến thức sẽ giúp bạn hiểu sâu hơn về môn Toán và giải quyết các bài tập khó khăn hơn.
Các kiến thức về đại số có ứng dụng rất lớn trong thực tế, từ việc tính toán các khoản chi tiêu hàng ngày đến việc giải quyết các bài toán kỹ thuật phức tạp. Việc nắm vững kiến thức về đại số sẽ giúp bạn tự tin hơn trong cuộc sống và công việc.
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải quyết thành công Mục 3 trang 25 SGK Toán 8 tập 1 – Chân trời sáng tạo. Hãy tiếp tục luyện tập và học hỏi để đạt được kết quả tốt nhất trong môn Toán.
| Bài tập | Hướng dẫn |
|---|---|
| Bài 1 | Rút gọn biểu thức... |
| Bài 2 | Tính giá trị của biểu thức... |