Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 58, 59 sách giáo khoa Toán 8 Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải cụ thể, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Cho một tam giác vuông có hai cạnh góc vuông là (a), (b) và cạnh huyền là (c).
Video hướng dẫn giải
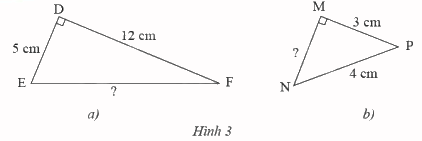
Tính độ dài cạnh \(EF\), \(MN\) của các tam giác vuông trong hình 3.
Phương pháp giải:
Sử dụng định lý Pythagore để tính độ dài các cạnh còn lại của tam giác vuông.
Lời giải chi tiết:
a) Áp dụng định lý Pythagore vào tam giác vuông \(DEF\) ta có:
\(E{F^2} = D{E^2} + D{F^2}\)
\(E{F^2} = {5^2} + {12^2} = 25 + 144 = 169 = {13^2}\)
Vậy \(EF = 13\) (cm)
b) Áp dụng định lý Pythagore vào tam giác vuông \(MNP\) ta có:
\(M{N^2} + M{P^2} = N{P^2}\)
\(M{N^2} + {3^2} = {4^2}\)
\(M{N^2} + 9 = 16\)
\(M{N^2} = 16 - 9 = 7\)
\(MN = \sqrt 7 \) (cm)
Video hướng dẫn giải
Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là \(72\)cm và \(120\)cm. Tính độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch (biết 1 inch \( \approx \)\(2,54\)cm).

Phương pháp giải:
Sử dụng định lý Pythagore tính độ dài đường chéo của màn hình chiếc tivi.
Lời giải chi tiết:
Gọi \(a\), \(b\), \(c\) là độ dài chiều dài, chiều rộng và đường chéo của tivi (đơn vị: cm)
Áp dụng định lí Pythagore ta có:
\({c^2} = {a^2} + {b^2}\)
\({c^2} = {120^2} + {72^2} = 14400 + 5184 = 19584\)
\(c = 24\sqrt {34} \) (cm)
Độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch là:
\(24\sqrt {34} :2,54 \approx 54\) (inch)
Video hướng dẫn giải
Cho một tam giác vuông có hai cạnh góc vuông là \(a\), \(b\) và cạnh huyền là \(c\).
- Lấy một tờ bìa lớn, cắt tám hình tam giác vuông bằng tam giác vuông đã cho và cắt hai hình vuông lớn có cùng có cạnh bằng \(a + b\).
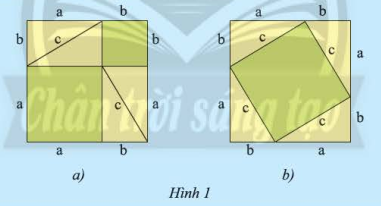
- Đặt bốn tam giác vuông lên hình vuông thứ nhất trong Hình 1a. Phần bìa không bị che lấp gồm hai hình vuông có cạnh lần lượt là \(a\) và \(b\). Tính diện tích phần bìa đó là \(a\) và \(b\).
- Đặt bốn tam giác vuông còn lại lên hình vuông thứ hai như trong Hình 1b. Phần bìa không bị che lấp là hình vuông có cạnh là \(c\). Tính diện tích phần bìa đó theo \(c\).
- Rút ra kết luận về quan hệ giữa \({a^2} + {b^2}\) và \({c^2}\).
Phương pháp giải:
Sử dụng công thức rồi tính diện tích theo yêu cầu
Lời giải chi tiết:
- Diện tích hai hình vuông màu xanh trong hình 1a là: \({a^2} + {b^2}\)
- Diện tích hình vuông màu xanh trong hình 1b là: \({c^2}\)
- Vậy \({a^2} + {b^2} = {c^2}\)
Video hướng dẫn giải
Cho một tam giác vuông có hai cạnh góc vuông là \(a\), \(b\) và cạnh huyền là \(c\).
- Lấy một tờ bìa lớn, cắt tám hình tam giác vuông bằng tam giác vuông đã cho và cắt hai hình vuông lớn có cùng có cạnh bằng \(a + b\).
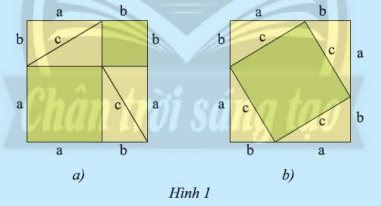
- Đặt bốn tam giác vuông lên hình vuông thứ nhất trong Hình 1a. Phần bìa không bị che lấp gồm hai hình vuông có cạnh lần lượt là \(a\) và \(b\). Tính diện tích phần bìa đó là \(a\) và \(b\).
- Đặt bốn tam giác vuông còn lại lên hình vuông thứ hai như trong Hình 1b. Phần bìa không bị che lấp là hình vuông có cạnh là \(c\). Tính diện tích phần bìa đó theo \(c\).
- Rút ra kết luận về quan hệ giữa \({a^2} + {b^2}\) và \({c^2}\).
Phương pháp giải:
Sử dụng công thức rồi tính diện tích theo yêu cầu
Lời giải chi tiết:
- Diện tích hai hình vuông màu xanh trong hình 1a là: \({a^2} + {b^2}\)
- Diện tích hình vuông màu xanh trong hình 1b là: \({c^2}\)
- Vậy \({a^2} + {b^2} = {c^2}\)
Video hướng dẫn giải
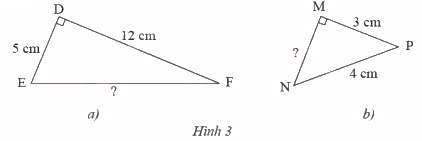
Tính độ dài cạnh \(EF\), \(MN\) của các tam giác vuông trong hình 3.
Phương pháp giải:
Sử dụng định lý Pythagore để tính độ dài các cạnh còn lại của tam giác vuông.
Lời giải chi tiết:
a) Áp dụng định lý Pythagore vào tam giác vuông \(DEF\) ta có:
\(E{F^2} = D{E^2} + D{F^2}\)
\(E{F^2} = {5^2} + {12^2} = 25 + 144 = 169 = {13^2}\)
Vậy \(EF = 13\) (cm)
b) Áp dụng định lý Pythagore vào tam giác vuông \(MNP\) ta có:
\(M{N^2} + M{P^2} = N{P^2}\)
\(M{N^2} + {3^2} = {4^2}\)
\(M{N^2} + 9 = 16\)
\(M{N^2} = 16 - 9 = 7\)
\(MN = \sqrt 7 \) (cm)
Video hướng dẫn giải
Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là \(72\)cm và \(120\)cm. Tính độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch (biết 1 inch \( \approx \)\(2,54\)cm).

Phương pháp giải:
Sử dụng định lý Pythagore tính độ dài đường chéo của màn hình chiếc tivi.
Lời giải chi tiết:
Gọi \(a\), \(b\), \(c\) là độ dài chiều dài, chiều rộng và đường chéo của tivi (đơn vị: cm)
Áp dụng định lí Pythagore ta có:
\({c^2} = {a^2} + {b^2}\)
\({c^2} = {120^2} + {72^2} = 14400 + 5184 = 19584\)
\(c = 24\sqrt {34} \) (cm)
Độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch là:
\(24\sqrt {34} :2,54 \approx 54\) (inch)
Mục 1 trang 58, 59 SGK Toán 8 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Đây là một phần quan trọng trong chương trình học Toán 8, giúp học sinh xây dựng nền tảng vững chắc cho các kiến thức nâng cao hơn.
Mục này bao gồm các bài tập về:
Bài tập 1 yêu cầu thu gọn các đa thức sau:
Giải:
Bài tập 2 yêu cầu tìm bậc của các đa thức sau:
Giải:
Bài tập 3 yêu cầu tính giá trị của đa thức P(x) = x2 - 2x + 1 tại x = -1.
Giải:
P(-1) = (-1)2 - 2(-1) + 1 = 1 + 2 + 1 = 4
Kiến thức về đa thức là nền tảng quan trọng cho việc học các kiến thức nâng cao hơn trong chương trình Toán học. Việc nắm vững các khái niệm và kỹ năng liên quan đến đa thức sẽ giúp học sinh giải quyết các bài toán phức tạp một cách dễ dàng và hiệu quả hơn.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập môn Toán. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 8 Chân trời sáng tạo, giúp các em học sinh học tập hiệu quả và đạt kết quả tốt nhất.
| Bài tập | Nội dung |
|---|---|
| Bài 1 | Thu gọn đa thức |
| Bài 2 | Tìm bậc của đa thức |
| Bài 3 | Tính giá trị của đa thức |