Bài 3 trang 62 SGK Toán 8 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào thực tế.
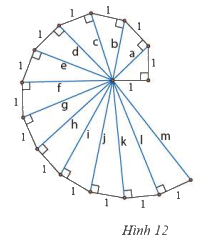
Lần lượt tính độ dài các cạnh huyền (a), (b), (c), (d) của các tam giác vuông trong Hình 12.
Đề bài
Lần lượt tính độ dài các cạnh huyền \(a\), \(b\), \(c\), \(d\) của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng định lý Pythagore tính độ dài các cạnh huyền
Lời giải chi tiết
Áp dụng định lý Pythagore vào các tam giác vuông trong hình ta có:
\({a^2} = {1^2} + {1^2} = 1 + 1 = 2\) . Suy ra \(a = \sqrt 2 \)
\({b^2} = {a^2} + {1^2} = 2 + 1 = 3\). Suy ra \(b = \sqrt 3 \)
\({c^2} = {b^2} + {1^2} = 3 + 1 = 4\). Suy ra \(c = \sqrt 4 \)
\({d^2} = {c^2} + {1^2} = 4 + 1 = 5\). Suy ra \(d = \sqrt 5 \)
Dự đoán:
\(e = \sqrt 6 \)
\(f = \sqrt 7 \)
\(g = \sqrt 8 \)
\(h = \sqrt 9 = 3\)
\(i = \sqrt {10} \)
\(k = \sqrt {11} \)
\(l = \sqrt {12} \)
\(m = \sqrt {13} \)
Bài 3 trang 62 SGK Toán 8 – Chân trời sáng tạo yêu cầu học sinh thực hiện các phép tính đại số, cụ thể là rút gọn biểu thức và tìm giá trị của biểu thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép tính, các quy tắc về dấu ngoặc, và các quy tắc về phép nhân, chia đa thức.
Bài 3 yêu cầu học sinh thực hiện các phép tính sau:
Để giải bài tập này, chúng ta sẽ sử dụng các công thức sau:
a) (3x + 2)(x – 1)
Áp dụng công thức (a + b)(c + d) = ac + ad + bc + bd, ta có:
(3x + 2)(x – 1) = 3x * x + 3x * (-1) + 2 * x + 2 * (-1) = 3x2 – 3x + 2x – 2 = 3x2 – x – 2
b) (2x – 3)(x + 4)
Áp dụng công thức (a + b)(c + d) = ac + ad + bc + bd, ta có:
(2x – 3)(x + 4) = 2x * x + 2x * 4 + (-3) * x + (-3) * 4 = 2x2 + 8x – 3x – 12 = 2x2 + 5x – 12
c) (x – 5)(x + 5)
Áp dụng công thức (a + b)(a – b) = a2 – b2, ta có:
(x – 5)(x + 5) = x2 – 52 = x2 – 25
d) (x – 2)2
Áp dụng công thức (a – b)2 = a2 – 2ab + b2, ta có:
(x – 2)2 = x2 – 2 * x * 2 + 22 = x2 – 4x + 4
Vậy, kết quả của các phép tính là:
Khi giải các bài tập về phép tính đại số, học sinh cần chú ý:
Để rèn luyện thêm kỹ năng về phép tính đại số, học sinh có thể làm thêm các bài tập tương tự sau:
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập, cung cấp các lời giải chi tiết, dễ hiểu và phương pháp giải toán hiệu quả. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác.