Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 – Chân trời sáng tạo. Mục 3 trang 9 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các phép toán cơ bản và cách áp dụng vào giải quyết bài tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn dễ dàng tiếp thu kiến thức và tự tin giải các bài tập tương tự.
Cho hai hình hộp chữ nhật A và B có các kích thước như hình 3. a) Tính tổng thể tích của hình hộp chữ nhật A và B. b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.
Video hướng dẫn giải
Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.
a) \(xy\) và \( - 6xy\)
b) \(2xy\) và \(x{y^2}\)
c) \( - 4yz{x^2}\) và \(4{x^2}yz\)
Phương pháp giải:
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác \(0\) và có cùng phần biến
Để cộng, trừ (hay tìm tổng, hiệu) hai đơn thức đồng dạng, ta cộng, trừ hệ số của chúng là giữ nguyên phần biến.
Lời giải chi tiết:
a) \(xy\) và \( - 6xy\) là hai đơn thức đồng dạng vì có hệ số khác \(0\) và có cùng phần biến là \(xy\).
Ta có:
\(xy + \left( { - 6xy} \right) = xy - 6xy = \left( {1 - 6} \right)xy = - 5xy\)
\(xy - \left( { - 6xy} \right) = xy + 6xy = \left( {1 + 6} \right)xy = 7xy\)
b) \(2xy\) và \(x{y^2}\) không là hai đơn thức đồng dạng.
c) \( - 4yz{x^2}\) và \(4{x^2}yz\) là hai đơn thức đồng dạng vì có hệ số khác 0 và có cùng phần biến là \({x^2}yz\).
Ta có:
\( - 4yz{x^2} + 4{x^2}yz = \left( { - 4 + 4} \right){x^2}yz = 0\)
\( - 4yz{x^2} - 4{x^2} = \left( { - 4 - 4} \right){x^2}yz = - 8{x^2}yz\)
Video hướng dẫn giải
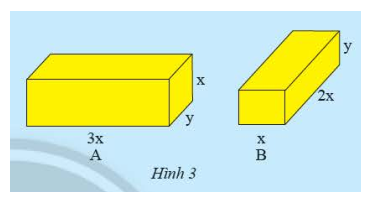
Cho hai hình hộp chữ nhật A và B có các kích thước như hình 3.
a) Tính tổng thể tích của hình hộp chữ nhật A và B.
b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.
Phương pháp giải:
Thể tích hình hộp chữ nhật là lượng không gian mà hình chiếm, được tính bằng tích của diện tích đáy và chiều cao: \(V = a.b.h\), trong đó \(a\), \(b\), \(h\), \(V\) lần lượt là chiều dài, chiều rộng, chiều cao và thể tích của hình hộp chữ nhật.
Lời giải chi tiết:
a) Thể tích của hình hộp chữ nhật A là: \({V_A} = 3x.y.x = 3.{x^2}y\)
Thể tích của hình hộp chữ nhật B là: \({V_B} = 2x.x.y = 2{x^2}y\)
Tổng thể tích của hình hộp chữ nhật A và B là: \(3{x^2}y + 2{x^2}y = \left( {3 + 2} \right).{x^2}y = 5{x^2}y\)
b) Biểu thức biểu diễn sự chênh lệch thể tích của A và B là: \(3{x^2}y - 2{x^2}y = \left( {3 - 2} \right).{x^2}y = {x^2}y\)
Video hướng dẫn giải
Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.
a) \(xy\) và \( - 6xy\)
b) \(2xy\) và \(x{y^2}\)
c) \( - 4yz{x^2}\) và \(4{x^2}yz\)
Phương pháp giải:
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác \(0\) và có cùng phần biến
Để cộng, trừ (hay tìm tổng, hiệu) hai đơn thức đồng dạng, ta cộng, trừ hệ số của chúng là giữ nguyên phần biến.
Lời giải chi tiết:
a) \(xy\) và \( - 6xy\) là hai đơn thức đồng dạng vì có hệ số khác \(0\) và có cùng phần biến là \(xy\).
Ta có:
\(xy + \left( { - 6xy} \right) = xy - 6xy = \left( {1 - 6} \right)xy = - 5xy\)
\(xy - \left( { - 6xy} \right) = xy + 6xy = \left( {1 + 6} \right)xy = 7xy\)
b) \(2xy\) và \(x{y^2}\) không là hai đơn thức đồng dạng.
c) \( - 4yz{x^2}\) và \(4{x^2}yz\) là hai đơn thức đồng dạng vì có hệ số khác 0 và có cùng phần biến là \({x^2}yz\).
Ta có:
\( - 4yz{x^2} + 4{x^2}yz = \left( { - 4 + 4} \right){x^2}yz = 0\)
\( - 4yz{x^2} - 4{x^2} = \left( { - 4 - 4} \right){x^2}yz = - 8{x^2}yz\)
Video hướng dẫn giải
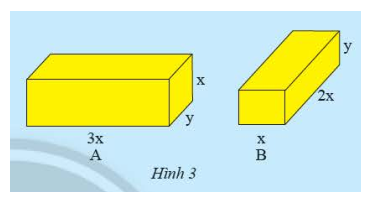
Cho hai hình hộp chữ nhật A và B có các kích thước như hình 3.
a) Tính tổng thể tích của hình hộp chữ nhật A và B.
b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.
Phương pháp giải:
Thể tích hình hộp chữ nhật là lượng không gian mà hình chiếm, được tính bằng tích của diện tích đáy và chiều cao: \(V = a.b.h\), trong đó \(a\), \(b\), \(h\), \(V\) lần lượt là chiều dài, chiều rộng, chiều cao và thể tích của hình hộp chữ nhật.
Lời giải chi tiết:
a) Thể tích của hình hộp chữ nhật A là: \({V_A} = 3x.y.x = 3.{x^2}y\)
Thể tích của hình hộp chữ nhật B là: \({V_B} = 2x.x.y = 2{x^2}y\)
Tổng thể tích của hình hộp chữ nhật A và B là: \(3{x^2}y + 2{x^2}y = \left( {3 + 2} \right).{x^2}y = 5{x^2}y\)
b) Biểu thức biểu diễn sự chênh lệch thể tích của A và B là: \(3{x^2}y - 2{x^2}y = \left( {3 - 2} \right).{x^2}y = {x^2}y\)
Mục 3 trang 9 SGK Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về phép cộng, trừ, nhân, chia số hữu tỉ. Đây là nền tảng quan trọng để học sinh tiếp thu các kiến thức nâng cao hơn trong chương trình Toán 8.
Mục 3 trang 9 bao gồm các bài tập vận dụng các phép toán cơ bản trên số hữu tỉ vào các tình huống thực tế. Các bài tập này giúp học sinh rèn luyện kỹ năng tính toán, tư duy logic và khả năng giải quyết vấn đề.
Đây là dạng bài tập cơ bản nhất, yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia số hữu tỉ theo đúng thứ tự ưu tiên.
Ví dụ: Tính giá trị của biểu thức: (1/2) + (3/4) - (5/8)
Giải: (1/2) + (3/4) - (5/8) = (4/8) + (6/8) - (5/8) = (4+6-5)/8 = 5/8
Dạng bài tập này yêu cầu học sinh vận dụng kiến thức về số hữu tỉ để giải quyết các bài toán thực tế, ví dụ như bài toán về diện tích, chu vi, thời gian, vận tốc,...
Ví dụ: Một mảnh đất hình chữ nhật có chiều dài 12m và chiều rộng 8m. Tính diện tích của mảnh đất đó.
Giải: Diện tích của mảnh đất hình chữ nhật là: 12m * 8m = 96m2
Dạng bài tập này yêu cầu học sinh sử dụng các phép toán để biến đổi phương trình và tìm ra giá trị của x.
Ví dụ: Giải phương trình: x + (1/3) = (5/6)
Giải: x = (5/6) - (1/3) = (5/6) - (2/6) = 3/6 = 1/2
Giaitoan.edu.vn là một website học Toán online uy tín, cung cấp:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học Toán 8 hữu ích và đạt kết quả cao trong học tập!
| Phép toán | Quy tắc |
|---|---|
| Cộng | Nếu hai số hữu tỉ có cùng mẫu số thì cộng các tử số và giữ nguyên mẫu số. Nếu hai số hữu tỉ có khác mẫu số thì quy đồng mẫu số rồi cộng. |
| Trừ | Nếu hai số hữu tỉ có cùng mẫu số thì trừ các tử số và giữ nguyên mẫu số. Nếu hai số hữu tỉ có khác mẫu số thì quy đồng mẫu số rồi trừ. |
| Nhân | Nhân các tử số với nhau và nhân các mẫu số với nhau. |
| Chia | Chia số hữu tỉ thứ nhất cho số hữu tỉ thứ hai là nhân số hữu tỉ thứ nhất với nghịch đảo của số hữu tỉ thứ hai. |