Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập mục 2 trang 44, 45 SGK Toán 8 tập 1 – Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 8, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
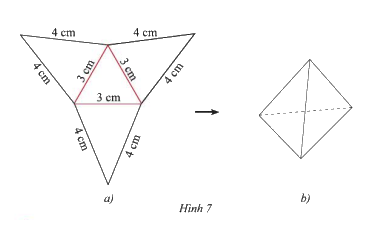
Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3cm và cạnh bên 4cm theo hướng dẫn sau: - Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a. - Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.
Video hướng dẫn giải
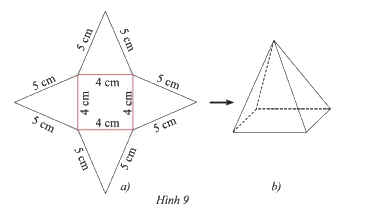
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
Phương pháp giải:
Thực hiên các bước làm theo hướng dẫn
Lời giải chi tiết:
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.
Video hướng dẫn giải
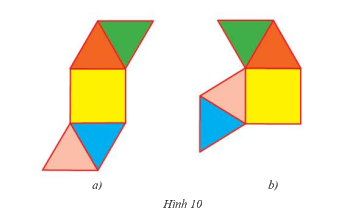
Tấm bìa nào sau đây có thể gấp thành hình chóp tứ giác đều
Phương pháp giải:
- Trên một tấm bìa, vẽ một hình vuông và 4 hình tam giác cân như hình 10a, 10b
- Gấp hai hình lại rồi tìm hình chóp tứ giác đều
Lời giải chi tiết:
- Trên một tấm bìa, vẽ một hình vuông và 4 hình tam giác cân như hình 10a, 10b
- Gấp hai hình lại ta thấy tấm bìa Hình 10a có thể gấp thành hình chóp tứ giác đều?
Video hướng dẫn giải
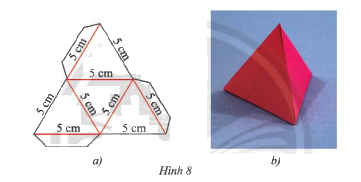
Cắt gấp và dán hộp quà hình chóp tam giác đều có độ dài cạnh đáy và cạnh bên bằng 5cm.
Gợi ý: Cắt theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.
Phương pháp giải:
- Trên một tấm bìa, vẽ 4 hình tam giác đều với kích thước như Hình 8a.
- Cắt tấm bìa theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.
Lời giải chi tiết:
- Trên một tấm bìa, vẽ 4 hình tam giác đều với kích thước như Hình 8a.
- Cắt tấm bìa theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.
- Sau khi gấp xong thu được hộp quà như Hình 8b
Video hướng dẫn giải
Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3cm và cạnh bên 4cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.
Phương pháp giải:
Tiến hành các bước theo hướng dẫn
Lời giải chi tiết:
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như hình 7b.
Video hướng dẫn giải
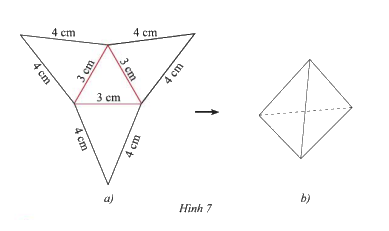
Tạo lập hình chóp tam giác đều có độ dài cạnh đáy 3cm và cạnh bên 4cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình tam giác đều và ba hình tam giác cân với kích thước như Hình 7a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tam giác đều như Hình 7b.
Phương pháp giải:
Tiến hành các bước theo hướng dẫn
Lời giải chi tiết:
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như hình 7b.
Video hướng dẫn giải
Cắt gấp và dán hộp quà hình chóp tam giác đều có độ dài cạnh đáy và cạnh bên bằng 5cm.
Gợi ý: Cắt theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.
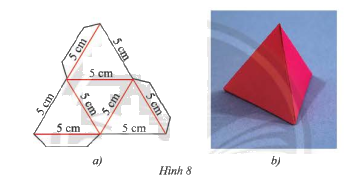
Phương pháp giải:
- Trên một tấm bìa, vẽ 4 hình tam giác đều với kích thước như Hình 8a.
- Cắt tấm bìa theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.
Lời giải chi tiết:
- Trên một tấm bìa, vẽ 4 hình tam giác đều với kích thước như Hình 8a.
- Cắt tấm bìa theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.
- Sau khi gấp xong thu được hộp quà như Hình 8b
Video hướng dẫn giải
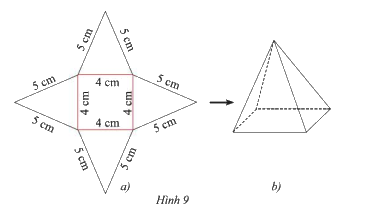
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
Phương pháp giải:
Thực hiên các bước làm theo hướng dẫn
Lời giải chi tiết:
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.
Video hướng dẫn giải
Tấm bìa nào sau đây có thể gấp thành hình chóp tứ giác đều
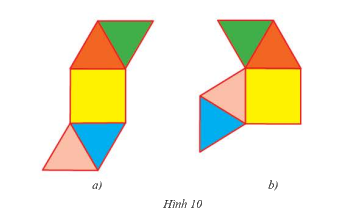
Phương pháp giải:
- Trên một tấm bìa, vẽ một hình vuông và 4 hình tam giác cân như hình 10a, 10b
- Gấp hai hình lại rồi tìm hình chóp tứ giác đều
Lời giải chi tiết:
- Trên một tấm bìa, vẽ một hình vuông và 4 hình tam giác cân như hình 10a, 10b
- Gấp hai hình lại ta thấy tấm bìa Hình 10a có thể gấp thành hình chóp tứ giác đều?
Mục 2 của chương trình Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các quy tắc cộng, trừ, nhân, chia đa thức, phân thức để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và kỹ năng biến đổi đại số là yếu tố then chốt để hoàn thành tốt các bài tập này.
Bài tập 1 yêu cầu học sinh thực hiện phép cộng hai đa thức. Để giải bài tập này, học sinh cần xác định các hạng tử đồng dạng trong hai đa thức và cộng các hệ số của chúng lại với nhau. Ví dụ, nếu có hai đa thức A = 2x2 + 3x - 1 và B = -x2 + 5x + 2, thì A + B = (2x2 - x2) + (3x + 5x) + (-1 + 2) = x2 + 8x + 1.
Bài tập 2 yêu cầu học sinh thực hiện phép trừ hai đa thức. Tương tự như phép cộng, học sinh cần xác định các hạng tử đồng dạng và trừ các hệ số của chúng. Ví dụ, nếu A = 3x2 - 2x + 4 và B = x2 + x - 1, thì A - B = (3x2 - x2) + (-2x - x) + (4 + 1) = 2x2 - 3x + 5.
Bài tập 3 yêu cầu học sinh thực hiện phép nhân hai đa thức. Để giải bài tập này, học sinh cần áp dụng quy tắc phân phối: mỗi hạng tử của đa thức thứ nhất nhân với mỗi hạng tử của đa thức thứ hai. Ví dụ, nếu A = x + 2 và B = x - 3, thì A * B = x(x - 3) + 2(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6.
Bài tập 4 yêu cầu học sinh thực hiện phép chia hai đa thức. Để giải bài tập này, học sinh có thể sử dụng phương pháp chia đa thức một cách thông thường hoặc sử dụng lược đồ Horner. Ví dụ, nếu A = x2 + 5x + 6 và B = x + 2, thì A / B = x + 3.
Bài tập 5 thường là một bài toán ứng dụng, yêu cầu học sinh vận dụng các kiến thức về đa thức, phân thức để giải quyết một vấn đề thực tế. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các đại lượng cần tìm và thiết lập phương trình hoặc hệ phương trình phù hợp.
Việc giải bài tập mục 2 trang 44, 45 SGK Toán 8 tập 1 – Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức về đa thức, phân thức đại số và kỹ năng biến đổi đại số. Hy vọng với lời giải chi tiết và các lưu ý trên, học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Bình phương của một hiệu |
| a2 - b2 = (a + b)(a - b) | Hiệu hai bình phương |