Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết mục 3 trang 61 SGK Toán 8 – Chân trời sáng tạo, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, kèm theo các ví dụ minh họa để bạn dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Tính các độ dài (PN) và (BC) trong Hình 9.
Video hướng dẫn giải
Tính chiều dài cần cẩu \(AB\) trong Hình 10.
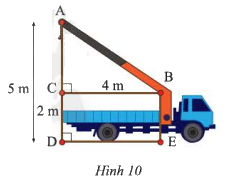
Phương pháp giải:
Tính độ dài \(AC\)
Sử dụng định lý Pythagore tính chiều dài cần cẩu
Lời giải chi tiết:
\(AC = AD - CD = 5 - 2 = 3\) (m)
Áp dụng định lý Pythagore vào tam giác vuông \(ABC\) ta có:
\(A{B^2} = A{C^2} + B{C^2}\)
\(A{B^2} = {3^2} + {4^2} = 9 + 16 = 25 = {5^2}\)
\(AB = 5\)(m)
Vậy chiều dài cần cẩu \(AB\) là 5m
Video hướng dẫn giải
Tính các độ dài \(PN\) và \(BC\) trong Hình 9.
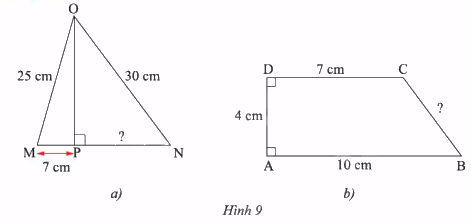
Phương pháp giải:
a. Sử dụng định lý Pythagore tính độ dài đoạn thẳng \(OP\), \(PN\).
b. Kẻ đường cao CH, sử dụng định lý Pythagore tính độ dài đoạn thẳng \(BC\).
Lời giải chi tiết:
a) Áp dụng định lý Pythagore vào tam giác vuông \(OMP\) ta có:
\(O{P^2} + M{P^2} = O{M^2}\)
\(O{P^2} + {7^2} = {25^2}\)
\(O{P^2} + 49 = 625\)
\(O{P^2} = 625 - 49 = 576 = {24^2}\)
\(OP = 24\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(OPN\) ta có:
\(P{N^2} + O{P^2} = O{N^2}\)
\(P{N^2} + {24^2} = {30^2}\)
\(P{N^2} = {30^2} - {24^2} = 324 = {18^2}\)
\(PN = 18\) (cm)
b) Kẻ đường cao \(CH\) như trong hình vẽ
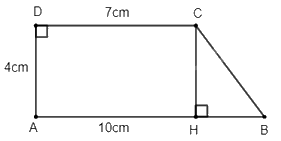
Ta có: \(CH = AD = 4\)cm; \(AH = CD = 7\)cm
\(BH = AB - AH = 10 - 7 = 3\)(cm)
Áp dụng định lý Pythagore vào tam giác vuông \(BCH\) ta có:
\(B{C^2} = C{H^2} + B{H^2}\)
\(B{C^2} = {4^2} + {3^2} = 16 + 9 = 25 = {5^2}\)
\(BC = 5\) (cm)
Video hướng dẫn giải
Tính các độ dài \(PN\) và \(BC\) trong Hình 9.
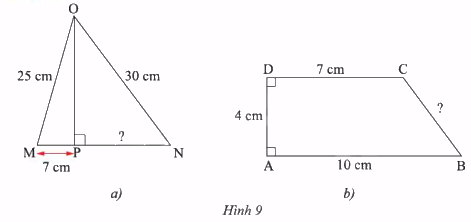
Phương pháp giải:
a. Sử dụng định lý Pythagore tính độ dài đoạn thẳng \(OP\), \(PN\).
b. Kẻ đường cao CH, sử dụng định lý Pythagore tính độ dài đoạn thẳng \(BC\).
Lời giải chi tiết:
a) Áp dụng định lý Pythagore vào tam giác vuông \(OMP\) ta có:
\(O{P^2} + M{P^2} = O{M^2}\)
\(O{P^2} + {7^2} = {25^2}\)
\(O{P^2} + 49 = 625\)
\(O{P^2} = 625 - 49 = 576 = {24^2}\)
\(OP = 24\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(OPN\) ta có:
\(P{N^2} + O{P^2} = O{N^2}\)
\(P{N^2} + {24^2} = {30^2}\)
\(P{N^2} = {30^2} - {24^2} = 324 = {18^2}\)
\(PN = 18\) (cm)
b) Kẻ đường cao \(CH\) như trong hình vẽ
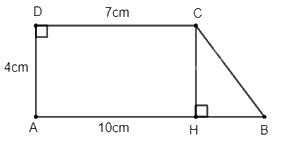
Ta có: \(CH = AD = 4\)cm; \(AH = CD = 7\)cm
\(BH = AB - AH = 10 - 7 = 3\)(cm)
Áp dụng định lý Pythagore vào tam giác vuông \(BCH\) ta có:
\(B{C^2} = C{H^2} + B{H^2}\)
\(B{C^2} = {4^2} + {3^2} = 16 + 9 = 25 = {5^2}\)
\(BC = 5\) (cm)
Video hướng dẫn giải
Tính chiều dài cần cẩu \(AB\) trong Hình 10.
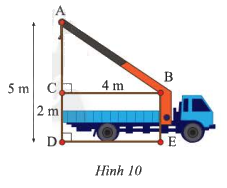
Phương pháp giải:
Tính độ dài \(AC\)
Sử dụng định lý Pythagore tính chiều dài cần cẩu
Lời giải chi tiết:
\(AC = AD - CD = 5 - 2 = 3\) (m)
Áp dụng định lý Pythagore vào tam giác vuông \(ABC\) ta có:
\(A{B^2} = A{C^2} + B{C^2}\)
\(A{B^2} = {3^2} + {4^2} = 9 + 16 = 25 = {5^2}\)
\(AB = 5\)(m)
Vậy chiều dài cần cẩu \(AB\) là 5m
Mục 3 trang 61 SGK Toán 8 – Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến các kiến thức đã học trong chương. Để giải quyết các bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, các định lý và các phương pháp giải toán đã được học.
Mục 3 trang 61 thường bao gồm các dạng bài tập sau:
Đề bài: Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Lời giải:
Áp dụng định lý Pitago vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42 = 9 + 16 = 25
BC = √25 = 5cm
Vậy, độ dài cạnh BC là 5cm.
Đề bài: Cho hình bình hành ABCD, có góc A = 60o, AB = 5cm, AD = 3cm. Tính diện tích hình bình hành ABCD.
Lời giải:
Kẻ đường cao AH vuông góc với DC. Trong tam giác ADH vuông tại H, ta có:
sin A = AH/AD
AH = AD * sin A = 3 * sin 60o = 3 * (√3/2) = (3√3)/2 cm
Diện tích hình bình hành ABCD là:
S = DC * AH = AB * AH = 5 * (3√3)/2 = (15√3)/2 cm2
Để giải các bài tập trong Mục 3 trang 61 SGK Toán 8 – Chân trời sáng tạo một cách nhanh chóng và hiệu quả, bạn nên:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn nên làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Bạn cũng có thể tìm kiếm các bài tập trực tuyến trên giaitoan.edu.vn để luyện tập.
Hy vọng rằng, với lời giải chi tiết và các hướng dẫn cụ thể trong bài viết này, bạn đã có thể tự tin giải quyết Mục 3 trang 61 SGK Toán 8 – Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!
| Dạng bài | Phương pháp giải |
|---|---|
| Áp dụng định lý | Xác định đúng định lý cần sử dụng và áp dụng vào bài toán. |
| Kết hợp kiến thức | Phân tích bài toán, xác định các kiến thức liên quan và kết hợp chúng để giải quyết. |
| Nâng cao | Tư duy sáng tạo, vận dụng linh hoạt kiến thức và tìm ra cách giải mới. |