Bài 2 trang 26 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh áp dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 2 trang 26 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
a) Vẽ đồ thị của hàm số (y = x) và (y = x + 2) trên cùng một mặt phẳng tọa độ. b) Dùng thước đo góc để tìm góc tạo bởi hai đường thẳng (y = x) và (y = x + 2) với trục (Ox).
Đề bài
a) Vẽ đồ thị của hàm số \(y = x\) và \(y = x + 2\) trên cùng một mặt phẳng tọa độ.
b) Dùng thước đo góc để tìm góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\). Đồ thị hàm số \(y = ax\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(A\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(B\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A\) và \(B\). Đồ thị của hàm số \(y = ax + b\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
Lời giải chi tiết
a)
- Vẽ đồ thị hàm số \(y = x\).
Cho \(x = 1 \Rightarrow y = 1 \Rightarrow \)Đồ thị hàm số đi qua điểm \(M\left( {1;1} \right)\).
Đồ thị hàm số \(y = x\) là đường thẳng đi qua hai điểm \(O\) và \(M\).
- Vẽ đồ thị hàm số \(y = x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) ta được điểm \(A\left( {0;2} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 2}}{1} = - 2\) ta được điểm \(B\left( { - 2;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
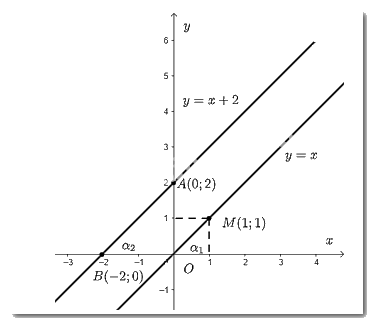
b) Góc tạo bởi hai đường thẳng \(y = x\) và \(y = x + 2\) với trục \(Ox\) lần lượt là \({\alpha _1}\) và \({\alpha _2}\).
Dùng thước đo độ kiểm tra ta thấy số đo \({\alpha _1} = {\alpha _2} = 45^\circ \).
Bài 2 trang 26 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về phép nhân đa thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc nhân đa thức, đặc biệt là quy tắc nhân đơn thức với đa thức và quy tắc nhân đa thức với đa thức.
Bài 2 yêu cầu học sinh thực hiện các phép nhân đa thức, thường là nhân một đơn thức với một đa thức hoặc nhân hai đa thức với nhau. Các bài tập có thể có dạng:
Để giải Bài 2 trang 26 SGK Toán 8 tập 2, học sinh có thể áp dụng các phương pháp sau:
Ví dụ 1: Tính (2x + 3)(x - 1)
Giải:
(2x + 3)(x - 1) = 2x(x - 1) + 3(x - 1) = 2x2 - 2x + 3x - 3 = 2x2 + x - 3
Ví dụ 2: Rút gọn biểu thức: 5x2 - 2x(x + 3)
Giải:
5x2 - 2x(x + 3) = 5x2 - 2x2 - 6x = 3x2 - 6x
Để củng cố kiến thức về phép nhân đa thức, học sinh có thể tự giải các bài tập tương tự sau:
Bài 2 trang 26 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về phép nhân đa thức. Bằng cách nắm vững các quy tắc và phương pháp giải, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Quy tắc | Ví dụ |
|---|---|
| Nhân đơn thức với đa thức | a(b + c) = ab + ac |
| Nhân đa thức với đa thức | (a + b)(c + d) = ac + ad + bc + bd |