Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 – Chân trời sáng tạo. Mục 4 trang 21 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải bài tập này, giúp bạn tự tin chinh phục môn Toán.
Sử dụng quy tắc chuyển vế và các tính chất của phép toán, hoàn thành các biến đổi sau vào vở
Video hướng dẫn giải
Sử dụng quy tắc chuyển vế và các tính chất của phép toán, hoàn thành các biến đổi sau vào vở:
\(\begin{array}{l}{\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\\{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\; = ...\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\\{a^3} - {b^3} = {\left( {a - b} \right)^3} + 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a - b} \right)^3} + 3ab\left( {a - b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\; = ...\end{array}\)
Phương pháp giải:
Áp dụng quy tắc chuyển vế, các tính chất của phép toán, hằng đẳng thức: Bình phương của một tổng, một hiệu.
Lời giải chi tiết:
\(\begin{array}{l}{\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\\{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left[ {{{\left( {a + b} \right)}^2} - 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left[ {{a^2} + 2ab + {b^2} - 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\\{a^3} - {b^3} = {\left( {a - b} \right)^3} + 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a - b} \right)^3} + 3ab\left( {a - b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left[ {{{\left( {a - b} \right)}^2} + 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left[ {{a^2} - 2ab + {b^2} + 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\end{array}\)
Video hướng dẫn giải
Viết các đa thức sau dưới dạng tích:
a) \(8{y^3} + 1\)
b) \({y^3} - 8\)
Phương pháp giải:
Biến đổi đa thức về dạng tổng, hiệu của hai lập phương rồi áp dụng hằng đẳng thức tổng, hiệu của hai lập phương.
Lời giải chi tiết:
a) \(8{y^3} + 1 = {\left( {2y} \right)^3} + {1^3} = \left( {2y + 1} \right)\left[ {{{\left( {2y} \right)}^2} - 2y.1 + {1^2}} \right] = \left( {2y + 1} \right)\left( {4{y^2} - 2y + 1} \right)\)
b) \({y^3} - 8 = {y^3} - {2^3} = \left( {y - 2} \right)\left( {{y^2} + 2y + {2^2}} \right) = \left( {y - 2} \right)\left( {{y^2} + 2y + 4} \right)\)
Video hướng dẫn giải
Tính:
a) \(\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)\)
b) \(\left( {2x - \dfrac{1}{2}} \right)\left( {4{x^2} + x + \dfrac{1}{4}} \right)\)
Phương pháp giải:
Biến đổi tích của hai đa thức về dạng vế phải của hằng đẳng thức: Tổng, hiệu của hai lập phương.
Lời giải chi tiết:
a) \(\left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = \left( {x + 1} \right)\left( {{x^2} - x.1 + {1^2}} \right) = {x^3} + {1^3} = {x^3} + 1\)
b) \(\left( {2x - \dfrac{1}{2}} \right)\left( {4{x^2} + x + \dfrac{1}{4}} \right) = \left( {2x - \dfrac{1}{2}} \right)\left[ {{{\left( {2x} \right)}^2} + 2x.\dfrac{1}{2} + {{\left( {\dfrac{1}{2}} \right)}^2}} \right] = {\left( {2x} \right)^3} - {\left( {\dfrac{1}{2}} \right)^3} = 8{x^3} - \dfrac{1}{8}\)
Video hướng dẫn giải
Sử dụng quy tắc chuyển vế và các tính chất của phép toán, hoàn thành các biến đổi sau vào vở:
\(\begin{array}{l}{\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\\{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\; = ...\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\\{a^3} - {b^3} = {\left( {a - b} \right)^3} + 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a - b} \right)^3} + 3ab\left( {a - b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {...} \right)\\\;\;\;\;\;\;\;\;\;\; = ...\end{array}\)
Phương pháp giải:
Áp dụng quy tắc chuyển vế, các tính chất của phép toán, hằng đẳng thức: Bình phương của một tổng, một hiệu.
Lời giải chi tiết:
\(\begin{array}{l}{\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\\{a^3} + {b^3} = {\left( {a + b} \right)^3} - 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left[ {{{\left( {a + b} \right)}^2} - 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left[ {{a^2} + 2ab + {b^2} - 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\\{a^3} - {b^3} = {\left( {a - b} \right)^3} + 3{a^2}b - 3a{b^2}\\\;\;\;\;\;\;\;\;\;\; = {\left( {a - b} \right)^3} + 3ab\left( {a - b} \right)\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left[ {{{\left( {a - b} \right)}^2} + 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left[ {{a^2} - 2ab + {b^2} + 3ab} \right]\\\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\end{array}\)
Video hướng dẫn giải
Viết các đa thức sau dưới dạng tích:
a) \(8{y^3} + 1\)
b) \({y^3} - 8\)
Phương pháp giải:
Biến đổi đa thức về dạng tổng, hiệu của hai lập phương rồi áp dụng hằng đẳng thức tổng, hiệu của hai lập phương.
Lời giải chi tiết:
a) \(8{y^3} + 1 = {\left( {2y} \right)^3} + {1^3} = \left( {2y + 1} \right)\left[ {{{\left( {2y} \right)}^2} - 2y.1 + {1^2}} \right] = \left( {2y + 1} \right)\left( {4{y^2} - 2y + 1} \right)\)
b) \({y^3} - 8 = {y^3} - {2^3} = \left( {y - 2} \right)\left( {{y^2} + 2y + {2^2}} \right) = \left( {y - 2} \right)\left( {{y^2} + 2y + 4} \right)\)
Video hướng dẫn giải
Tính:
a) \(\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)\)
b) \(\left( {2x - \dfrac{1}{2}} \right)\left( {4{x^2} + x + \dfrac{1}{4}} \right)\)
Phương pháp giải:
Biến đổi tích của hai đa thức về dạng vế phải của hằng đẳng thức: Tổng, hiệu của hai lập phương.
Lời giải chi tiết:
a) \(\left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = \left( {x + 1} \right)\left( {{x^2} - x.1 + {1^2}} \right) = {x^3} + {1^3} = {x^3} + 1\)
b) \(\left( {2x - \dfrac{1}{2}} \right)\left( {4{x^2} + x + \dfrac{1}{4}} \right) = \left( {2x - \dfrac{1}{2}} \right)\left[ {{{\left( {2x} \right)}^2} + 2x.\dfrac{1}{2} + {{\left( {\dfrac{1}{2}} \right)}^2}} \right] = {\left( {2x} \right)^3} - {\left( {\dfrac{1}{2}} \right)^3} = 8{x^3} - \dfrac{1}{8}\)
Video hướng dẫn giải
Từ một khối lập phương có cạnh bằng \(2x + 1\), ta cắt bỏ một khối lập phương có cạnh bằng \(x + 1\) (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.
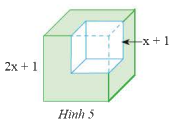
Phương pháp giải:
Áp dụng công thức tính thể tích của hình lập phương
Áp dụng hằng đẳng thức: Hiệu của hai lập phương
Lời giải chi tiết:
Thể tích phần còn lại của khối lập phương là:
\(\begin{array}{l}{\left( {2x + 1} \right)^3} - {\left( {x + 1} \right)^3}\\ = \left[ {\left( {2x + 1} \right) - \left( {x + 1} \right)} \right].\left[ {{{\left( {2x + 1} \right)}^2} + \left( {2x + 1} \right)\left( {x + 1} \right) + {{\left( {x + 1} \right)}^2}} \right]\\ = x.\left[ {4{x^2} + 4x + 1 + 2{x^2} + 2x + x + 1 + {x^2} + 2x + 1} \right]\\ = x.\left( {7{x^2} + 9x + 3} \right)\\ = 7{x^3} + 9{x^2} + 3x\end{array}\)
Video hướng dẫn giải
Từ một khối lập phương có cạnh bằng \(2x + 1\), ta cắt bỏ một khối lập phương có cạnh bằng \(x + 1\) (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.
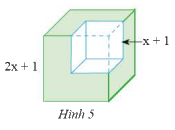
Phương pháp giải:
Áp dụng công thức tính thể tích của hình lập phương
Áp dụng hằng đẳng thức: Hiệu của hai lập phương
Lời giải chi tiết:
Thể tích phần còn lại của khối lập phương là:
\(\begin{array}{l}{\left( {2x + 1} \right)^3} - {\left( {x + 1} \right)^3}\\ = \left[ {\left( {2x + 1} \right) - \left( {x + 1} \right)} \right].\left[ {{{\left( {2x + 1} \right)}^2} + \left( {2x + 1} \right)\left( {x + 1} \right) + {{\left( {x + 1} \right)}^2}} \right]\\ = x.\left[ {4{x^2} + 4x + 1 + 2{x^2} + 2x + x + 1 + {x^2} + 2x + 1} \right]\\ = x.\left( {7{x^2} + 9x + 3} \right)\\ = 7{x^3} + 9{x^2} + 3x\end{array}\)
Mục 4 trang 21 SGK Toán 8 tập 1 – Chân trời sáng tạo thường tập trung vào các bài toán liên quan đến các phép biến đổi đại số đơn giản, các biểu thức đại số và việc rút gọn biểu thức. Để giải quyết các bài toán này một cách hiệu quả, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất của phép cộng, trừ, nhân, chia và các quy tắc về dấu ngoặc.
Bài 1 thường yêu cầu học sinh thực hiện các phép tính trên các biểu thức đại số. Ví dụ:
Để giải bài này, học sinh cần áp dụng các quy tắc về phép cộng, trừ các đơn thức đồng dạng. Ví dụ, trong biểu thức 3x + 2y – x + 5y, ta có thể rút gọn bằng cách cộng các đơn thức đồng dạng 3x và -x, 2y và 5y, để được 2x + 7y.
Bài 2 thường yêu cầu học sinh giải các phương trình bậc nhất một ẩn. Ví dụ:
Giải phương trình: 2x + 5 = 11
Để giải bài này, học sinh cần áp dụng các quy tắc về chuyển vế và cộng trừ hai vế của phương trình. Ví dụ, ta có thể chuyển 5 sang vế phải của phương trình, được 2x = 11 – 5, hay 2x = 6. Sau đó, ta chia cả hai vế cho 2, được x = 3.
Bài 3 thường yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán thực tế. Ví dụ:
Một người mua 3 cái áo sơ mi với giá x đồng một cái và 2 cái quần với giá y đồng một cái. Tổng số tiền người đó phải trả là 200.000 đồng. Hãy viết biểu thức đại số biểu thị tổng số tiền người đó phải trả và tính giá trị của biểu thức khi x = 50.000 đồng và y = 80.000 đồng.
Để giải bài này, học sinh cần hiểu rõ đề bài và xác định được các đại lượng liên quan. Biểu thức đại số biểu thị tổng số tiền người đó phải trả là 3x + 2y. Khi x = 50.000 đồng và y = 80.000 đồng, giá trị của biểu thức là 3 * 50.000 + 2 * 80.000 = 150.000 + 160.000 = 310.000 đồng.
Ngoài SGK Toán 8 tập 1 – Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Giải mục 4 trang 21 SGK Toán 8 tập 1 – Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức cơ bản về đại số và luyện tập thường xuyên. Hy vọng với những hướng dẫn chi tiết và hữu ích trên đây, các bạn học sinh sẽ tự tin chinh phục môn Toán và đạt kết quả tốt nhất.