Giải bài 8 trang 81 SGK Toán 8 tập 1 – Chân trời sáng tạo

Giải bài 8 trang 81 SGK Toán 8 tập 1– Chân trời sáng tạo

Giải bài 8 trang 81 SGK Toán 8 tập 1 – Chân trời sáng tạo

Bài 8 trang 81 SGK Toán 8 tập 1 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 81 SGK Toán 8 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.

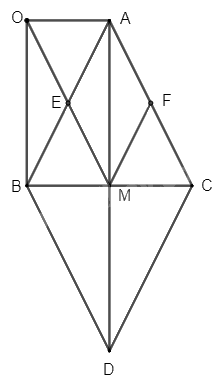
Cho tam giác

Đề bài

Cho tam giác \(ABC\) cân tại \(A\), gọi \(M\) là trung điểm của \(BC\). Lấy điểm \(D\) đối xứng với điểm \(A\) qua \(BC\).

a) Chứng minh tứ giác \(ABDC\) là hình thoi

b) Gọi \(E\), \(F\) lần lượt là trung điểm của \(AB\) và \(AC\), lấy điểm \(O\) sao cho \(E\) là trung điểm của \(OM\). Chứng minh rằng hai tam giác \(AOB\) và \(MBO\) bằng nhau

c) Chứng minh tứ giác \(AEMF\) là hình thoi

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài 8 trang 81 SGK Toán 8 tập 1– Chân trời sáng tạo 1

a) Áp dụng dấu hiệu nhận biết của hình thoi

b) Sử dụng tính chất của tam giác cân, chứng minh \(AM\) vuông góc với \(BC\). Chứng minh \(OAMB\) là hình bình hành

Chứng minh \(OB\) // \(AM\)

Chứng minh \(\Delta AOB = \Delta MBO\) (hai tam giác vuông)

c) Áp dụng dấu hiệu nhận biết của hình thoi

Lời giải chi tiết

Giải bài 8 trang 81 SGK Toán 8 tập 1– Chân trời sáng tạo 2

a) Xét tứ giác \(ABDC\) có:

\(M\) là trung điểm của \(BC\) (gt)

\(M\) là trung điểm của \(AD\) (do \(D\) đối xứng với \(A\) qua \(BC\))

Suy ra \(ABDC\) là hình bình hành

Ta có tam giác ABC là tam giác cân nên AB = AC.

Suy ra \(ABDC\) là hình thoi (hình bình hành có hai cạnh kề bằng nhau)

b) Do \(\Delta ABC\) cân tại \(A\), có \(AM\) là trung tuyến (gt)

Suy ra \(AM\) là đường cao, trung trực, phân giác

Suy ra \(AM\) vuông góc \(BM\) và \(CM\)

Xét tứ giác \(OAMB\) ta có:

\(E\) là trung điểm của \(OM\) và \(AB\) (gt)

Suy ra \(OAMB\) là hình bình hành

Suy ra \(OB\) // \(AM\); \(OA\) // \(MB\); \(OA = BM\); \(OB = AM\)

Mà \(AM \bot BM\) (cmt)

Suy ra: \(AM \bot OA\); \(OB \bot MB\)

Mà \(AM\) // \(OB\) (cmt)

Suy ra \(OB \bot OA\)

Xét \(\Delta AOB\) và \(\Delta MBO\) (các tam giác vuông) ta có:

\(\widehat {{\rm{AOB}}} = \widehat {{\rm{OBM}}} = 90^\circ \)

\(AO = MB\) (cmt)

\(OB = AM\) (cmt)

Suy ra \(\Delta AOB = \Delta MBO\) (c-g-c)

Suy ra \(OM = AB\)

c) \(OM = AB\) (cmt)

Mà \(EM = EO = \frac{1}{2}OM\); \(EA = EB = \frac{1}{2}AB\)

Suy ra \(EO = EA = EM = EB\) (1)

Xét \(\Delta ABC\) cân ta có: \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)

Mà \(EA = EB = \frac{1}{2}AB\); \(FA = FC = \frac{1}{2}AC\) (gt)

Suy ra \(AE = EB = FA = FM\) (2)

Xét \(\Delta BEM\) và \(\Delta CMF\) ta có:

\(BE = CF\) (cmt)

\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)

\(BM = CM\) (gt)

Suy ra \(\Delta BEM = \Delta CFM\) (c-g-c)

Suy ra \(EM = FM\) (3)

Từ (1), (2), (3) suy ra \(AE = AF = FM = ME\)

Suy ra \(AEMF\) là hình thoi

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 8 trang 81 SGK Toán 8 tập 1– Chân trời sáng tạo đặc sắc thuộc chuyên mục toán 8 sgk trên soạn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 8 trang 81 SGK Toán 8 tập 1 – Chân trời sáng tạo: Tóm tắt lý thuyết và phương pháp giải

Bài 8 trang 81 SGK Toán 8 tập 1 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số, đặc biệt là các quy tắc cộng, trừ, nhân, chia đa thức để giải quyết bài toán. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như đơn thức, đa thức, bậc của đa thức, hệ số của đa thức, và các phép toán trên đa thức.

Nội dung bài 8 trang 81 SGK Toán 8 tập 1 – Chân trời sáng tạo

Bài 8 thường bao gồm các dạng bài tập sau:

Dạng 1: Thực hiện các phép toán cộng, trừ, nhân, chia đa thức.
Dạng 2: Rút gọn biểu thức đại số.
Dạng 3: Tìm giá trị của biểu thức đại số tại một giá trị cụ thể của biến.
Dạng 4: Chứng minh đẳng thức đại số.

Lời giải chi tiết bài 8 trang 81 SGK Toán 8 tập 1 – Chân trời sáng tạo

Để giúp học sinh hiểu rõ hơn về cách giải bài 8 trang 81 SGK Toán 8 tập 1, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Ở đây sẽ là nội dung giải chi tiết từng câu hỏi của bài 8, ví dụ:)

Ví dụ 1: Thực hiện phép tính (2x + 3)(x - 1)

Để thực hiện phép tính này, chúng ta sử dụng quy tắc nhân hai đa thức:

(2x + 3)(x - 1) = 2x(x - 1) + 3(x - 1) = 2x² - 2x + 3x - 3 = 2x² + x - 3

Ví dụ 2: Rút gọn biểu thức 3x² + 2x - 5x² + 4x

Để rút gọn biểu thức này, chúng ta thực hiện các phép cộng, trừ các đơn thức đồng dạng:

3x² + 2x - 5x² + 4x = (3x² - 5x²) + (2x + 4x) = -2x² + 6x

Mẹo giải bài tập về phép biến đổi đại số

Để giải các bài tập về phép biến đổi đại số một cách nhanh chóng và chính xác, học sinh nên:

Nắm vững các quy tắc cộng, trừ, nhân, chia đa thức.
Sử dụng các công thức biến đổi đại số một cách linh hoạt.
Kiểm tra lại kết quả sau khi giải xong.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.

Ứng dụng của kiến thức về phép biến đổi đại số

Kiến thức về phép biến đổi đại số có ứng dụng rất lớn trong nhiều lĩnh vực khác nhau, như:

Giải các bài toán đại số.
Xây dựng các mô hình toán học.
Phân tích dữ liệu.
Lập trình máy tính.

Bài tập luyện tập thêm

Để củng cố kiến thức về phép biến đổi đại số, học sinh có thể làm thêm các bài tập sau:

Rút gọn biểu thức: (x + 2)(x - 3)
Tìm giá trị của biểu thức 2x² - 5x + 3 tại x = 2
Chứng minh đẳng thức: (x + y)² = x² + 2xy + y²

Kết luận

Bài 8 trang 81 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán 8.