Chào mừng bạn đến với bài học về Lý thuyết Tọa độ của một điểm và đồ thị của hàm số trong chương trình Toán 8 - Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hệ tọa độ, cách xác định tọa độ của một điểm và cách vẽ đồ thị của hàm số.
Chúng tôi sẽ trình bày lý thuyết một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể và bài tập thực hành để giúp bạn nắm vững kiến thức. Hãy cùng bắt đầu!
Tọa độ của một điểm là gì?
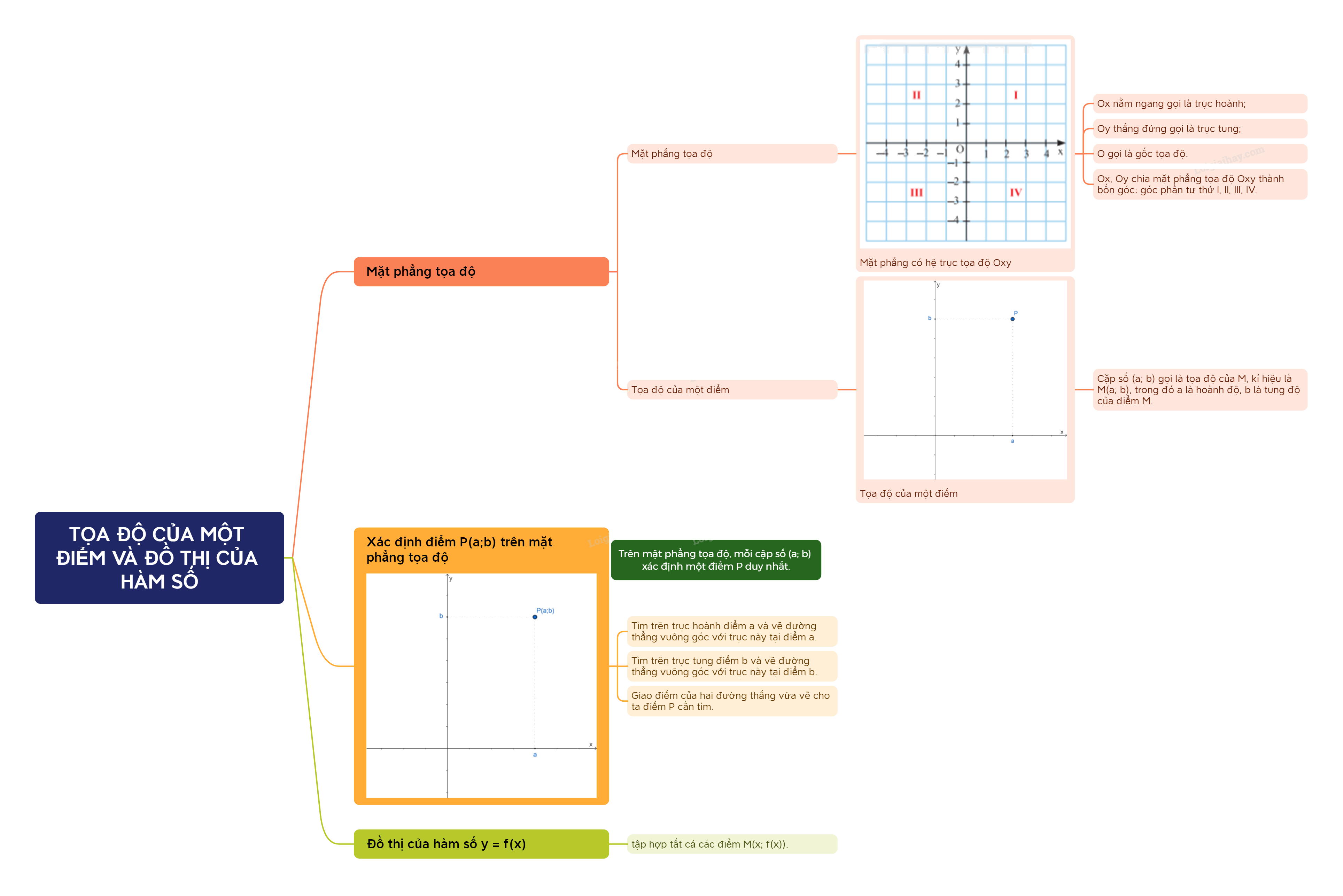
1. Tọa độ của một điểm
a. Khái niệm:
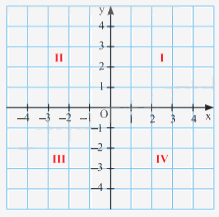
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.
Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: góc phần tư thứ I, II, III, IV.
b. Tọa độ của một điểm:
Trong mặt phẳng tọa độ, mỗi điểm P xác định duy nhất một cặp số (a; b) và mỗi cặp số (a; b) xác định duy nhất một điểm M.
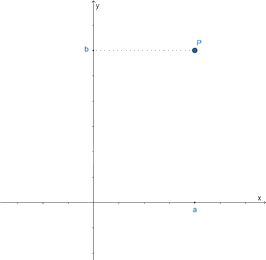
Cặp số (a; b) gọi là tọa độ của M, kí hiệu là M(a; b), trong đó a là hoành độ, b là tung độ của điểm M.
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.
2. Xác địnhmột điểm trên mặt phẳng tọa độ khi biết tọa độ của nó
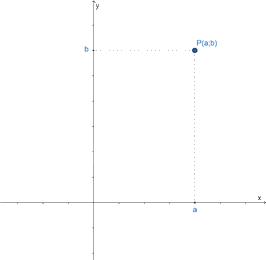
Để xác định một điểm điểm P có tọa độ là (a; b), ta thực hiện các bước sau:
- Tìm trên trục hoành điểm a và vẽ đường thẳng vuông góc với trục này tại điểm a.
- Tìm trên trục tung điểm b và vẽ đường thẳng vuông góc với trục này tại điểm b.
- Giao điểm của hai đường thẳng vừa vẽ cho ta điểm P cần tìm.
Chú ý: Trên mặt phẳng tọa độ, mỗi cặp số (a; b) xác định một điểm P duy nhất.
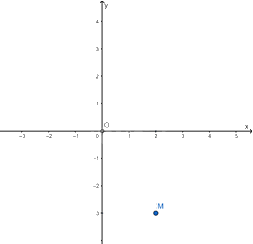
Ví dụ: Biểu diễn điểm M(2; -3) trên mặt phẳng tọa độ Oxy
3. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) trên mặt phẳng tọa độ Oxy là tập hợp tất cả các điểm M(x; f(x)).
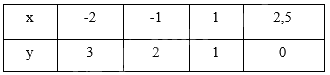
Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng:

Trong chương trình Toán 8, việc nắm vững kiến thức về tọa độ điểm và đồ thị hàm số là vô cùng quan trọng. Đây là nền tảng cho các kiến thức nâng cao hơn trong các lớp học tiếp theo. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về chủ đề này, dựa trên sách giáo khoa Toán 8 - Chân trời sáng tạo.
Hệ tọa độ là một công cụ quan trọng trong hình học, cho phép chúng ta xác định vị trí của một điểm trong mặt phẳng bằng cách sử dụng hai số, gọi là tọa độ. Hệ tọa độ thường được biểu diễn bằng hai trục vuông góc nhau, trục hoành (Ox) và trục tung (Oy). Giao điểm của hai trục này là gốc tọa độ (O).
Một điểm M trong mặt phẳng có tọa độ (x; y), trong đó x là hoành độ và y là tung độ. Hoành độ là khoảng cách từ điểm M đến trục tung, còn tung độ là khoảng cách từ điểm M đến trục hoành.
Để xác định tọa độ của một điểm M, ta thực hiện các bước sau:
Đồ thị của một hàm số là tập hợp tất cả các điểm trên mặt phẳng tọa độ mà tọa độ của chúng thỏa mãn phương trình của hàm số đó. Để vẽ đồ thị của một hàm số, ta thực hiện các bước sau:
Ví dụ 1: Xác định tọa độ của điểm A trên hình vẽ sau (hình vẽ minh họa hệ tọa độ và điểm A).
Giải: Dựa vào hình vẽ, ta thấy hoành độ của điểm A là 3 và tung độ của điểm A là 2. Vậy tọa độ của điểm A là (3; 2).
Ví dụ 2: Vẽ đồ thị của hàm số y = 2x + 1.
Giải:
| x | y = 2x + 1 |
|---|---|
| -2 | -3 |
| -1 | -1 |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
Vẽ hệ tọa độ và đánh dấu các điểm (-2; -3), (-1; -1), (0; 1), (1; 3), (2; 5) lên hệ tọa độ. Nối các điểm này lại với nhau, ta được đồ thị của hàm số y = 2x + 1.
Hi vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về Lý thuyết Tọa độ của một điểm và đồ thị của hàm số trong chương trình Toán 8 - Chân trời sáng tạo. Việc nắm vững kiến thức này sẽ là bước đệm quan trọng cho việc học tập các môn học khác liên quan đến toán học và khoa học.