Giải Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo

Chào mừng các em học sinh đến với lời giải chi tiết Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về bài học.

Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học Toán 8 một cách hiệu quả và dễ dàng.

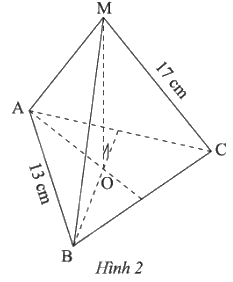
Quan sát hình chóp tạm giác đều ở Hình 2 và cho biết

Đề bài

Quan sát hình chóp tam giác đều ở Hình 2 và cho biết:

a) Đỉnh, mặt đáy và các mặt bên của hình đó

b) Độ dài cạnh \(MA\) và cạnh \(BC\)

c) Đoạn thẳng nào là đường cao của hình đó.

Giải Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo 2

Sử dụng kiến thức về hình chóp tam giác đều để tìm đỉnh, mặt đáy, cạnh bên, cạnh đáy, đường cao

Lời giải chi tiết

a) Đỉnh: \(M\)

Mặt đáy: \(ABC\)

Các mặt bên: \(MAB\); \(MAC\); \(MBC\)

b) Các cạnh bên bằng nhau: \(MA = MC = 17\)cm

Các cạnh đáy bằng nhau: \(BC = AB = 13\)cm

c) Đoạn thẳng \(MO\) là đường cao của hình chóp tam giác đều \(M.ABC\)

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo đặc sắc thuộc chuyên mục toán 8 trên đề thi toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo: Tổng quan

Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức đã học về đa thức, đơn thức để giải các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các quy tắc cộng, trừ, nhân, chia đa thức, đơn thức, cũng như các phép biến đổi tương đương.

Nội dung chi tiết Bài 7

Bài 7 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:

Thực hiện các phép tính với đa thức và đơn thức.
Rút gọn biểu thức đại số.
Tìm giá trị của biểu thức tại một giá trị cụ thể của biến.
Vận dụng kiến thức đã học để giải các bài toán có tính ứng dụng.

Hướng dẫn giải chi tiết

Để giải Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo một cách hiệu quả, các em cần:

Đọc kỹ đề bài và xác định yêu cầu của bài toán.
Xác định các đa thức và đơn thức cần thực hiện các phép tính.
Vận dụng các quy tắc cộng, trừ, nhân, chia đa thức, đơn thức để thực hiện các phép tính.
Rút gọn biểu thức đại số bằng cách sử dụng các phép biến đổi tương đương.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Ví dụ minh họa

Ví dụ 1: Thực hiện phép tính: (3x² + 2x - 1) + (x² - 3x + 2)

Giải:

(3x² + 2x - 1) + (x² - 3x + 2) = 3x² + 2x - 1 + x² - 3x + 2 = (3x² + x²) + (2x - 3x) + (-1 + 2) = 4x² - x + 1

Lưu ý quan trọng

Khi thực hiện các phép tính với đa thức và đơn thức, các em cần chú ý đến:

Dấu của các số hạng.
Bậc của đa thức.
Các quy tắc cộng, trừ, nhân, chia đa thức, đơn thức.

Bài tập luyện tập

Để củng cố kiến thức và kỹ năng giải Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo, các em có thể tự giải thêm các bài tập sau:

Rút gọn biểu thức: 2x² + 3x - 1 - (x² - x + 2)
Tìm giá trị của biểu thức: 4x² - 5x + 1 tại x = 2
Giải phương trình: 3x + 2 = 0

Kết luận

Bài 7 trang 55 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về đa thức, đơn thức và các phép toán đại số. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!

Bảng tổng hợp các công thức liên quan

Công thức	Mô tả
(a + b)² = a² + 2ab + b²	Bình phương của một tổng
(a - b)² = a² - 2ab + b²	Bình phương của một hiệu
a² - b² = (a + b)(a - b)	Hiệu hai bình phương