Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 50, 51, 52 sách giáo khoa Toán 8 tập 1 chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải các bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Bạn Hùng có một cái gàu có dạng hình chóp tứ giác đều
Video hướng dẫn giải
Tính thể tích của một chiếc hộp bánh ít có dạng hình chóp tứ giác đều, có độ dài cạnh đáy là 3cm và chiều cao là \(2,5\)cm.

Phương pháp giải:
Sử dụng công thức tính thể tích hình chóp
Lời giải chi tiết:
Diện tích đáy là: \(3.3 = 9\) (\(c{m^2}\))
Thể tích của hình chiếc hộp bánh là: \(\frac{1}{3}.9.2,5 = 7,5\) (\(c{m^3}\))
Video hướng dẫn giải
Hãy giải bài toán ở phần mở đầu (trang 49)
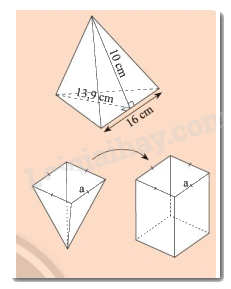
a) Bạn Mai cần dán giấy bóng kính màu xung quanh một chiếc lồng đèn hình chóp tam giác đều với kích thước như hình bên. Hỏi diện tích giấy mà Mai cần là bao nhiêu?
b) Bạn Hùng dùng một cái gàu hình chóp tứ giác đều để múc nước đổ vào một thùng chứa hình lăng trụ có cùng diện tích đáy và chiều cao như hình bên. Hãy dự đoán xem bạn Hùng phải đổ bào nhiêu gàu thì nước đầy thùng.
Phương pháp giải:
a) Sử dụng công thức tính diện tích toàn phần của hình chóp tam giác đều
b) Sử dụng công thức tính thể tích của hình lăng trụ đứng và hình chóp tứ giác đều.
Lời giải chi tiết:
a) Diện tích xung quanh của chiếc lồng là: \(10.3.16:2 = 240\) (\(c{m^2}\))
Diện tích đáy là: \(13,9.16:2 = 111,2\) (\(c{m^2}\))
Diện tích giấy mai cần là: \(240 + 111,2 = 351,2\) (\(c{m^2}\))
b) Gọi \(h\) là chiều cao của gàu nước và thùng chứa
Thể tích gàu nước là: \(V = \frac{1}{3}{a^2}h\)
Thể tích thùng chứa là: \(V = {a^2}h\)
Bạn Hùng phải đổ số gàu nước là: \({a^2}h:\left( {\frac{1}{3}{a^2}h} \right) = 3\) (gàu)
Video hướng dẫn giải
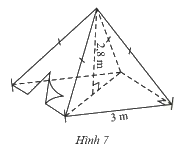
Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như Hình 7.
a) Tính thể tích không khí trong chiếc lều.
b) Tính diện tích vải lều (không tính các mép dán), biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là \(3,18\)m và lều này không có đáy.
Phương pháp giải:
a) Sử dụng công thức tính thể tích hình chóp tứ giác đều
b) Sử dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Lời giải chi tiết:
a) Thể tích không khí trong chiếc lều là: \(\frac{1}{3}{.3^2}.2,8 = 8,4\) (\({m^3}\))
b) Độ dài trung đoạn của hình chóp là: \(\sqrt {2,{8^2} + 1,{5^2}} \approx 3,18\)
Diện tích vải lều là: \(\frac{{4.3}}{2}.3,18= 19,08\) (\(c{m^2}\))
Video hướng dẫn giải
Bạn Hùng có một cái gàu có dạng hình chóp tứ giác đều và một cái thùng (không chứa nước) có dạng hình lăng trụ đứng. Hai vật này có cùng diện tích đáy và chiều cao (Hình 3a). Hùng múc đầy một gày nước và đổ vào thùng thì thấy chiều cao của cột nước bằng \(\frac{1}{3}\) chiều cao của thùng (Hình 3b). Gọi \(S\)đáy là diện tích đáy và \(h\) là chiều cao của cái gàu.
a) Tính thể tích \(V\) của phần nước đổ vào theo S đáy và \(h\).
b) Từ câu a), hãy dự đoán thể tích của cái gàu.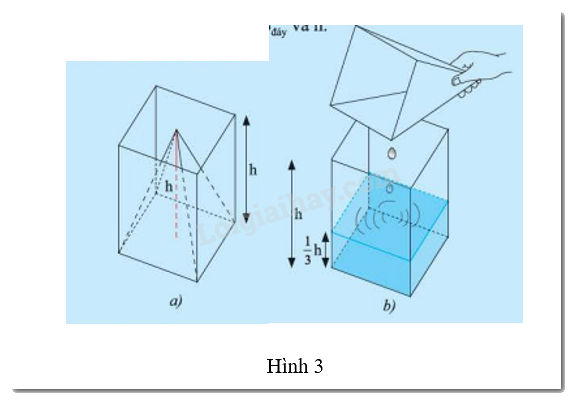
Phương pháp giải:
a) Áp dụng công thức tính thể tích hình hộp
b) Tính thể tích của gàu
Lời giải chi tiết:
a) Thể tích của phần nước là: \(V = \)Sđáy\(.\frac{1}{3}h\)\( = \frac{1}{3}hS\)đáy
b) Thể tích của cái gàu là: V\( = \frac{1}{3}hS\)đáy
Video hướng dẫn giải
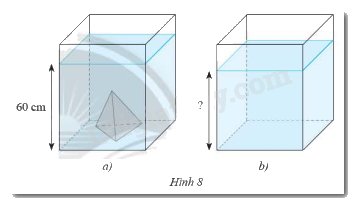
Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60\)cm và \(30\)cm. Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270c{m^2}\), chiều cao \(30\)cm. Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mực nước là \(60\)cm. Khi lấy khối đá ra thì mực nước của bể là bao nhiêu? Biết rằng bề dày của đáy bể và thành bể không đáng kể?
Phương pháp giải:
Tính thể tích mực nước lúc đầu, thể tích khối đá, thể tích nước lúc sau khi lấy khối đá ra
Tính chiều cao của mực nước sau khi lấy khối đá.
Lời giải chi tiết:
a) Thể tích của nước khi có khối đá là: \(60.30.60 = 108000\) (\(c{m^3}\))
Thể tích của khối đá là: \(\frac{1}{3}.270.30 = 2700\) (\(c{m^3}\))
Thể tích nước sau khi lấy khối đá là: \(108000 - 2700 = 105300\) (\(c{m^3}\))
Chiều cao mực nước là: \(105300:60:30 = 58,5\) (\(cm\))
Video hướng dẫn giải
Bạn Hùng có một cái gàu có dạng hình chóp tứ giác đều và một cái thùng (không chứa nước) có dạng hình lăng trụ đứng. Hai vật này có cùng diện tích đáy và chiều cao (Hình 3a). Hùng múc đầy một gày nước và đổ vào thùng thì thấy chiều cao của cột nước bằng \(\frac{1}{3}\) chiều cao của thùng (Hình 3b). Gọi \(S\)đáy là diện tích đáy và \(h\) là chiều cao của cái gàu.
a) Tính thể tích \(V\) của phần nước đổ vào theo S đáy và \(h\).
b) Từ câu a), hãy dự đoán thể tích của cái gàu.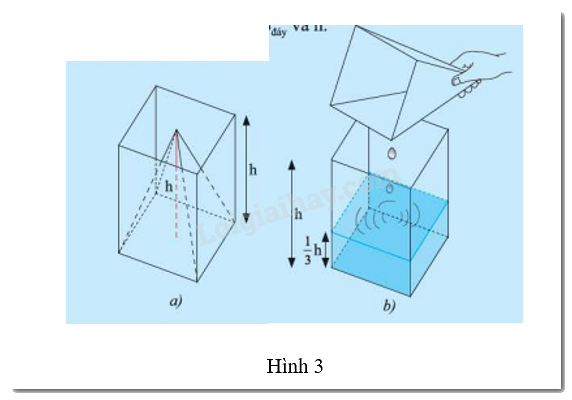
Phương pháp giải:
a) Áp dụng công thức tính thể tích hình hộp
b) Tính thể tích của gàu
Lời giải chi tiết:
a) Thể tích của phần nước là: \(V = \)Sđáy\(.\frac{1}{3}h\)\( = \frac{1}{3}hS\)đáy
b) Thể tích của cái gàu là: V\( = \frac{1}{3}hS\)đáy
Video hướng dẫn giải
Tính thể tích của một chiếc hộp bánh ít có dạng hình chóp tứ giác đều, có độ dài cạnh đáy là 3cm và chiều cao là \(2,5\)cm.

Phương pháp giải:
Sử dụng công thức tính thể tích hình chóp
Lời giải chi tiết:
Diện tích đáy là: \(3.3 = 9\) (\(c{m^2}\))
Thể tích của hình chiếc hộp bánh là: \(\frac{1}{3}.9.2,5 = 7,5\) (\(c{m^3}\))
Video hướng dẫn giải
Hãy giải bài toán ở phần mở đầu (trang 49)
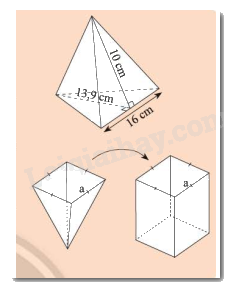
a) Bạn Mai cần dán giấy bóng kính màu xung quanh một chiếc lồng đèn hình chóp tam giác đều với kích thước như hình bên. Hỏi diện tích giấy mà Mai cần là bao nhiêu?
b) Bạn Hùng dùng một cái gàu hình chóp tứ giác đều để múc nước đổ vào một thùng chứa hình lăng trụ có cùng diện tích đáy và chiều cao như hình bên. Hãy dự đoán xem bạn Hùng phải đổ bào nhiêu gàu thì nước đầy thùng.
Phương pháp giải:
a) Sử dụng công thức tính diện tích toàn phần của hình chóp tam giác đều
b) Sử dụng công thức tính thể tích của hình lăng trụ đứng và hình chóp tứ giác đều.
Lời giải chi tiết:
a) Diện tích xung quanh của chiếc lồng là: \(10.3.16:2 = 240\) (\(c{m^2}\))
Diện tích đáy là: \(13,9.16:2 = 111,2\) (\(c{m^2}\))
Diện tích giấy mai cần là: \(240 + 111,2 = 351,2\) (\(c{m^2}\))
b) Gọi \(h\) là chiều cao của gàu nước và thùng chứa
Thể tích gàu nước là: \(V = \frac{1}{3}{a^2}h\)
Thể tích thùng chứa là: \(V = {a^2}h\)
Bạn Hùng phải đổ số gàu nước là: \({a^2}h:\left( {\frac{1}{3}{a^2}h} \right) = 3\) (gàu)
Video hướng dẫn giải
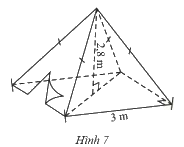
Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như Hình 7.
a) Tính thể tích không khí trong chiếc lều.
b) Tính diện tích vải lều (không tính các mép dán), biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là \(3,18\)m và lều này không có đáy.
Phương pháp giải:
a) Sử dụng công thức tính thể tích hình chóp tứ giác đều
b) Sử dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều.
Lời giải chi tiết:
a) Thể tích không khí trong chiếc lều là: \(\frac{1}{3}{.3^2}.2,8 = 8,4\) (\({m^3}\))
b) Độ dài trung đoạn của hình chóp là: \(\sqrt {2,{8^2} + 1,{5^2}} \approx 3,18\)
Diện tích vải lều là: \(\frac{{4.3}}{2}.3,18= 19,08\) (\(c{m^2}\))
Video hướng dẫn giải
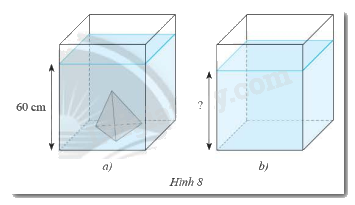
Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60\)cm và \(30\)cm. Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270c{m^2}\), chiều cao \(30\)cm. Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mực nước là \(60\)cm. Khi lấy khối đá ra thì mực nước của bể là bao nhiêu? Biết rằng bề dày của đáy bể và thành bể không đáng kể?
Phương pháp giải:
Tính thể tích mực nước lúc đầu, thể tích khối đá, thể tích nước lúc sau khi lấy khối đá ra
Tính chiều cao của mực nước sau khi lấy khối đá.
Lời giải chi tiết:
a) Thể tích của nước khi có khối đá là: \(60.30.60 = 108000\) (\(c{m^3}\))
Thể tích của khối đá là: \(\frac{1}{3}.270.30 = 2700\) (\(c{m^3}\))
Thể tích nước sau khi lấy khối đá là: \(108000 - 2700 = 105300\) (\(c{m^3}\))
Chiều cao mực nước là: \(105300:60:30 = 58,5\) (\(cm\))
Mục 2 của chương trình Toán 8 tập 1 – Chân trời sáng tạo thường tập trung vào các kiến thức cơ bản về đa thức, các phép toán trên đa thức, và ứng dụng của chúng trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài tập này yêu cầu học sinh vận dụng các quy tắc về thu gọn đa thức, bao gồm việc cộng, trừ các đơn thức đồng dạng. Để thu gọn đa thức, ta cần:
Ví dụ: Thu gọn đa thức 3x2 + 2x - 5x2 + x + 1. Ta có:
(3x2 - 5x2) + (2x + x) + 1 = -2x2 + 3x + 1
Bậc của đa thức là bậc của đơn thức có bậc cao nhất trong đa thức đó. Để tìm bậc của đa thức, ta cần:
Ví dụ: Tìm bậc của đa thức -2x2 + 3x + 1. Ta có:
Vậy bậc của đa thức -2x2 + 3x + 1 là 2.
Để tính giá trị của đa thức tại một giá trị cho trước, ta thay giá trị đó vào đa thức và thực hiện các phép tính.
Ví dụ: Tính giá trị của đa thức -2x2 + 3x + 1 tại x = 2. Ta có:
-2(2)2 + 3(2) + 1 = -2(4) + 6 + 1 = -8 + 6 + 1 = -1
Kiến thức về đa thức có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học kỹ thuật. Ví dụ:
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập nâng cao về đa thức. Các bài tập này thường yêu cầu vận dụng linh hoạt các kiến thức đã học và khả năng tư duy logic.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cần thiết để giải quyết các bài tập trong mục 2 trang 50, 51, 52 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc các em học tập tốt!