Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho từng bài tập trong SGK Toán 8 tập 1 – Chân trời sáng tạo, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 8 tập 1 tập trung vào các kiến thức quan trọng về đa thức. Việc hiểu rõ và vận dụng thành thạo các kiến thức này là nền tảng cho các bài học tiếp theo.
Hình 11a là hình chụp tấm lưới thép được
Video hướng dẫn giải
Một tứ giác có chu vi là \(52\) cm và một đường chéo là \(24\)cm. Tính độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
Phương pháp giải:
Chứng minh tứ giác là hình thoi
Tính độ dài cạnh, đường chéo
Lời giải chi tiết:
Do tứ giác có hai đường chéo vuông góc tại trung điểm của mỗi đường (gt)
Suy ra tứ giác là hình thoi
Độ dài cạnh là \(52:4 = 13\) (cm)
Do hình thoi có hai đường chéo vuông góc, tạo thành 4 tam giác vuông bằng nhau.
Độ dài nửa đường chéo còn lại là: \(\sqrt {{{13}^2} - {{\left( {24:2} \right)}^2}} = \sqrt {169 - 144} = \sqrt {25} = 5\) (cm)
Độ dài đường chéo còn lại là: \(5.2 = 10\) (cm)
Video hướng dẫn giải
Cho hình thoi \(MNPQ\) có \(I\) là giao điểm của hai đường chéo.
a) Tính \(MP\) khi biết \(MN = 10\)dm, \(IN = 6\)dm
b) Tính \(\widehat {{\rm{IMN}}}\) khi \(\widehat {{\rm{MNP}}} = 128^\circ \)
Phương pháp giải:
Sử dụng tính chất của hình thoi
Lời giải chi tiết:
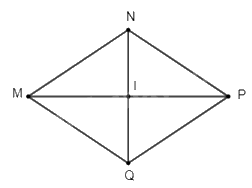
a) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(IM = IP\) và \(NQ \bot MP\)
Suy ra \(\widehat {{\rm{MIN}}} = 90\)
Xét tam giác vuông \(MPI\) (vuông tại \(I\)) ta có:
\(M{I^2} = M{N^2} - N{I^2} = {10^2} - {6^2} = 100 - 36 = 64\) (định lý Pythagore)
Suy ra \(MI = 8\) (dm)
b) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(NI\) là phân giác của \(\widehat {MNP}\)
Suy ra \(\widehat {MNI} = \widehat {PNI} = \frac{{128^\circ }}{2} = 64^\circ \)
Xét \(\Delta MNI\) vuông tại \(I\) ta có:
\(\widehat {{\rm{MNI}}} + \widehat {{\rm{NMI}}} = 90\)
Suy ra \(\widehat {IMN} = 90^\circ - \widehat {MNI} = 90^\circ - 64^\circ = 26^\circ \)
Video hướng dẫn giải
Cho \(ABCD\) là một hình bình hành. Giải thích tại sao tứ giác \(ABCD\) có bốn cạnh bằng nhau trong mỗi trường hợp sau:
Trường hợp 1: \(AB = AD\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là phân giác góc \(BAD\)
Trường hợp 4: \(BD\) là phân giác góc \(ABC\)
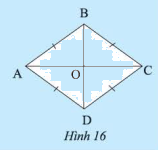
Phương pháp giải:
Áp dụng tính chất của hình bình hành
Lời giải chi tiết:
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra : \(AB = CD\); \(AD = BC\) (1)
\(O\) là trung điểm của \(AC\) và \(BD\)
TH1: Nếu \(AB = AD\) suy ra \(AB = BC = CD = AD\)
TH2: \(AC\) vuông góc với \(BD\)
Suy ra bốn tam giác vuông \(OAB\), \(OAD\), \(OCD\), \(COB\) bằng nhau
Suy ra \(AB = BC = CD = DA\)
TH3: \(AC\) là phân giác của góc \(BAD\)
Suy ra \(AO\) là phân giác của góc \(BAD\)
Mà \(AO\) là trung tuyến của \(\Delta ABD\)
Suy ra \(\Delta ABD\) cân tại \(A\)
Suy ra \(AB = AD\) (3)
Từ (1), (3) suy ra \(AB = BC = CD = DA\) TH4: Chứng minh tương tự
Video hướng dẫn giải
Một hoa văn trang trí được ghép bởi ba hình tứ giác có độ dài mỗi cạnh đều bằng 2cm (hình 18). Gọi tên các tứ giác này và tính chu vi của hoa văn.

Phương pháp giải:
Áp dụng dấu hiệu nhận biết của hình thoi
Lời giải chi tiết:
Các tứ giác trên là hình thoi vì có 4 cạnh bằng nhau
Chu vi của hoa văn là: \(2 \times 4 \times 3 = 24\) (cm)
Video hướng dẫn giải
a) Hình thoi có là hình bình hành không?
b) Cho hình thoi \(ABCD\) có \(O\) là giao điểm của hai đường chéo (Hình 13b). Các tam giác \(OAB\), \(OCB\), \(OCD\), \(OAD\) có bằng nhau không?
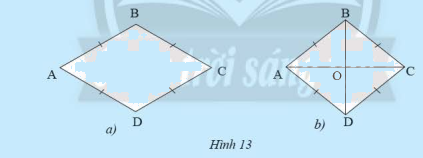
Phương pháp giải:
a) Áp dụng dấu hiệu nhận biết của hình bình hành
b) Áp dụng trường hợp bằng nhau thứ nhất của tam giác
Lời giải chi tiết:
a) Hình thoi cũng là hình bình hànhs
b) Vì \(ABCD\) là hình thoi (gt)
Suy ra \(ABCD\) cũng là hình bình hành
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Suy ra \(OA = OC\); \(OB = OD\)
Các tam giác \(OAB\); \(OCB\); \(OCD\); \(OAD\) bằng nhau theo trường hợp c-c-c
Video hướng dẫn giải
Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là ${3,2}$cm và ${2,4}$cm.
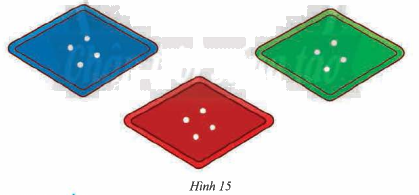
Phương pháp giải:
Sử dụng tính chất của hình thoi
Lời giải chi tiết:
Do hai đường chéo của hình thoi vuông góc với nhau tạo thành 4 tam giác vuông bằng nhau nên áp dụng định lý Pythagore vào mỗi tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{{3,2}}{2}} \right)}^2} + {{\left( {\frac{{2,4}}{2}} \right)}^2}} = \sqrt 4 = 2\) (cm)
Video hướng dẫn giải
Hình 11a là hình chụp tấm lưới thép được đan thành nhiều mắt. Hình 11b là hình vẽ phóng to của một mắt lưới. Đo độ dài các cạnh của tứ giác \(ABCD\) và rút ra nhận xét.

Phương pháp giải:
Sử dụng thước đo độ dài các cạnh của tứ giác
Lời giải chi tiết:
Các cạnh của tứ giác \(ABCD\) có độ dài bằng nhau
Video hướng dẫn giải
Hình 11a là hình chụp tấm lưới thép được đan thành nhiều mắt. Hình 11b là hình vẽ phóng to của một mắt lưới. Đo độ dài các cạnh của tứ giác \(ABCD\) và rút ra nhận xét.

Phương pháp giải:
Sử dụng thước đo độ dài các cạnh của tứ giác
Lời giải chi tiết:
Các cạnh của tứ giác \(ABCD\) có độ dài bằng nhau
Video hướng dẫn giải
a) Hình thoi có là hình bình hành không?
b) Cho hình thoi \(ABCD\) có \(O\) là giao điểm của hai đường chéo (Hình 13b). Các tam giác \(OAB\), \(OCB\), \(OCD\), \(OAD\) có bằng nhau không?

Phương pháp giải:
a) Áp dụng dấu hiệu nhận biết của hình bình hành
b) Áp dụng trường hợp bằng nhau thứ nhất của tam giác
Lời giải chi tiết:
a) Hình thoi cũng là hình bình hànhs
b) Vì \(ABCD\) là hình thoi (gt)
Suy ra \(ABCD\) cũng là hình bình hành
Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)
Suy ra \(OA = OC\); \(OB = OD\)
Các tam giác \(OAB\); \(OCB\); \(OCD\); \(OAD\) bằng nhau theo trường hợp c-c-c
Video hướng dẫn giải
Cho hình thoi \(MNPQ\) có \(I\) là giao điểm của hai đường chéo.
a) Tính \(MP\) khi biết \(MN = 10\)dm, \(IN = 6\)dm
b) Tính \(\widehat {{\rm{IMN}}}\) khi \(\widehat {{\rm{MNP}}} = 128^\circ \)
Phương pháp giải:
Sử dụng tính chất của hình thoi
Lời giải chi tiết:
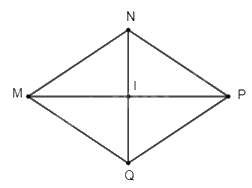
a) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(IM = IP\) và \(NQ \bot MP\)
Suy ra \(\widehat {{\rm{MIN}}} = 90\)
Xét tam giác vuông \(MPI\) (vuông tại \(I\)) ta có:
\(M{I^2} = M{N^2} - N{I^2} = {10^2} - {6^2} = 100 - 36 = 64\) (định lý Pythagore)
Suy ra \(MI = 8\) (dm)
b) Vì \(MNPQ\) là hình thoi (gt)
Suy ra \(NI\) là phân giác của \(\widehat {MNP}\)
Suy ra \(\widehat {MNI} = \widehat {PNI} = \frac{{128^\circ }}{2} = 64^\circ \)
Xét \(\Delta MNI\) vuông tại \(I\) ta có:
\(\widehat {{\rm{MNI}}} + \widehat {{\rm{NMI}}} = 90\)
Suy ra \(\widehat {IMN} = 90^\circ - \widehat {MNI} = 90^\circ - 64^\circ = 26^\circ \)
Video hướng dẫn giải
Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là ${3,2}$cm và ${2,4}$cm.

Phương pháp giải:
Sử dụng tính chất của hình thoi
Lời giải chi tiết:
Do hai đường chéo của hình thoi vuông góc với nhau tạo thành 4 tam giác vuông bằng nhau nên áp dụng định lý Pythagore vào mỗi tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{{3,2}}{2}} \right)}^2} + {{\left( {\frac{{2,4}}{2}} \right)}^2}} = \sqrt 4 = 2\) (cm)
Video hướng dẫn giải
Cho \(ABCD\) là một hình bình hành. Giải thích tại sao tứ giác \(ABCD\) có bốn cạnh bằng nhau trong mỗi trường hợp sau:
Trường hợp 1: \(AB = AD\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là phân giác góc \(BAD\)
Trường hợp 4: \(BD\) là phân giác góc \(ABC\)
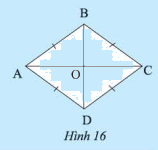
Phương pháp giải:
Áp dụng tính chất của hình bình hành
Lời giải chi tiết:
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra : \(AB = CD\); \(AD = BC\) (1)
\(O\) là trung điểm của \(AC\) và \(BD\)
TH1: Nếu \(AB = AD\) suy ra \(AB = BC = CD = AD\)
TH2: \(AC\) vuông góc với \(BD\)
Suy ra bốn tam giác vuông \(OAB\), \(OAD\), \(OCD\), \(COB\) bằng nhau
Suy ra \(AB = BC = CD = DA\)
TH3: \(AC\) là phân giác của góc \(BAD\)
Suy ra \(AO\) là phân giác của góc \(BAD\)
Mà \(AO\) là trung tuyến của \(\Delta ABD\)
Suy ra \(\Delta ABD\) cân tại \(A\)
Suy ra \(AB = AD\) (3)
Từ (1), (3) suy ra \(AB = BC = CD = DA\) TH4: Chứng minh tương tự
Video hướng dẫn giải
Một hoa văn trang trí được ghép bởi ba hình tứ giác có độ dài mỗi cạnh đều bằng 2cm (hình 18). Gọi tên các tứ giác này và tính chu vi của hoa văn.

Phương pháp giải:
Áp dụng dấu hiệu nhận biết của hình thoi
Lời giải chi tiết:
Các tứ giác trên là hình thoi vì có 4 cạnh bằng nhau
Chu vi của hoa văn là: \(2 \times 4 \times 3 = 24\) (cm)
Video hướng dẫn giải
Một tứ giác có chu vi là \(52\) cm và một đường chéo là \(24\)cm. Tính độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
Phương pháp giải:
Chứng minh tứ giác là hình thoi
Tính độ dài cạnh, đường chéo
Lời giải chi tiết:
Do tứ giác có hai đường chéo vuông góc tại trung điểm của mỗi đường (gt)
Suy ra tứ giác là hình thoi
Độ dài cạnh là \(52:4 = 13\) (cm)
Do hình thoi có hai đường chéo vuông góc, tạo thành 4 tam giác vuông bằng nhau.
Độ dài nửa đường chéo còn lại là: \(\sqrt {{{13}^2} - {{\left( {24:2} \right)}^2}} = \sqrt {169 - 144} = \sqrt {25} = 5\) (cm)
Độ dài đường chéo còn lại là: \(5.2 = 10\) (cm)
Mục 2 trong SGK Toán 8 tập 1 – Chân trời sáng tạo xoay quanh các kiến thức về đa thức, bao gồm các khái niệm cơ bản như đơn thức, đa thức, bậc của đa thức, các phép toán trên đa thức (cộng, trừ, nhân, chia) và các ứng dụng của đa thức trong giải toán.
Các bài tập trên trang 76 tập trung vào việc nhận biết đơn thức, xác định hệ số, phần biến và bậc của đơn thức. Các em cần nắm vững định nghĩa và các tính chất của đơn thức để giải quyết các bài tập này một cách chính xác.
Trang 77 giới thiệu khái niệm đa thức và các bài tập liên quan đến việc nhận biết đa thức, xác định bậc của đa thức và thu gọn đa thức. Việc phân biệt đơn thức và đa thức là rất quan trọng.
Các bài tập trên trang 78 hướng dẫn các em thực hiện các phép cộng, trừ đa thức. Để thực hiện các phép toán này, các em cần chú ý đến việc nhóm các hạng tử đồng dạng.
Ví dụ: Cộng hai đa thức P(x) = 2x2 + 3x - 1 và Q(x) = -x2 + 5x + 2. Ta có: P(x) + Q(x) = (2x2 - x2) + (3x + 5x) + (-1 + 2) = x2 + 8x + 1
Trang 79 bắt đầu giới thiệu các phép nhân, chia đa thức. Các bài tập ban đầu thường tập trung vào việc nhân một đơn thức với một đa thức hoặc nhân hai đơn thức.
| Bài tập | Nội dung |
|---|---|
| Bài 5 | Nhân các đơn thức sau: 2x2y.(-3xy2) |
| Bài 6 | Nhân một đơn thức với một đa thức: 2x(x2 - 3x + 1) |
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 76, 77, 78, 79 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc các em học tập tốt!