Chào mừng các em học sinh đến với lời giải chi tiết Bài 19 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình học tập và ôn luyện môn Toán.
Chúng tôi sẽ cung cấp đáp án đầy đủ, chính xác cùng với phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Cho hai hàm số (y = x + 3), (y = - x + 3) có đồ thị lần lượt là các đường thẳng ({d_1}) và ({d_2}).
b) Dùng thước đo góc để tìm góc tạo bởi \({d_1}\) và \({d_2}\) lần lượt với trục \(Ox\).
Phương pháp giải:
Đo góc
Lời giải chi tiết:
Gọi \({\alpha _1};{\alpha _2}\) lần lượt là 2 góc tạo bởi đường thẳng \({d_1};{d_2}\) với \(Ox\).
Dùng thước đo độ ta kiểm tra được\({\alpha _1} = 45^\circ ;{\alpha _2} = 135^\circ \).
c) Tính chu vi và diện tích của tam giác \(ABC\).
Phương pháp giải:
- Chu vi tam giác: \(C = a + b + c\) với \(a,b,c\) là ba cạnh tam giác.
- Diện tích tam giác: \(S = \dfrac{1}{2}a.{h_a}\) với \(a\) là độ dài đáy, \({h_a}\) là độ dài chiều cao tương ứng.
Lời giải chi tiết:
Vì \(Ox \bot Oy\) tại \(O\)nên tam giác \(AOB\) và tam giác \(AOC\) đều vuông tại \(O\).
Ta có: \(OA = 3;OB = 3;OC = 3\)
\(BC = OB + OC = 3 + 3 = 6\).
Áp dụng định lí Py – ta – go cho tam giác \(AOB\) ta có:
\(O{A^2} + O{B^2} = A{B^2}\)
\( \Leftrightarrow {3^2} + {3^2} = A{B^2}\)
\( \Leftrightarrow A{B^2} = 9 + 9 = 18\)
\( \Leftrightarrow AB = \sqrt {18} = 3\sqrt 2 \)
Áp dụng định lí Py – ta – go cho tam giác \(AOC\) ta có:
\(O{A^2} + O{C^2} = A{C^2}\)
\( \Leftrightarrow {3^2} + {3^2} = A{C^2}\)
\( \Leftrightarrow A{C^2} = 9 + 9 = 18\)
\( \Leftrightarrow AC = \sqrt {18} = 3\sqrt 2 \)
Chu vi tam giác \(ABC\) là:
\(C = AB + AC + BC = 3\sqrt 2 + 3\sqrt 2 + 6 = 6 + 6\sqrt 2 \) (đơn vị độ dài)
Vì \(Ox \bot Oy\) nên \(OA\) vuông góc với \(BC\) tại \(O\). Do đó, \(OA\) là đường cao tam giác \(ABC\) ứng với cạnh \(BC\).
Diện tích tam giác \(ABC\) là:
\(S = \dfrac{1}{2}OA.BC = \dfrac{1}{2}.3.6 = 9\) (đơn vị diện tích)
Vậy chu vi tam giác \(ABC\) là \(6 + 6\sqrt 2 \) đơn vị độ dài và diện tích tam giác \(ABC\) là 9 đơn vị diện tích.
Video hướng dẫn giải
Cho hai hàm số \(y = x + 3\), \(y = - x + 3\) có đồ thị lần lượt là các đường thẳng \({d_1}\) và \({d_2}\).
a) Bằng cách vẽ hình, tìm tọa độ giao điểm \(A\) của hai đường thẳng nói trên và tìm các giao điểm \(B,C\) lần lượt của \({d_1}\) và \({d_2}\) với trục \(Ox\).
Phương pháp giải:
- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).
Lời giải chi tiết:
- Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
- Vẽ đồ thị hàm số \(y = - x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{{ - 1}} = 3\) ta được điểm \(C\left( {3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = - x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(C\).
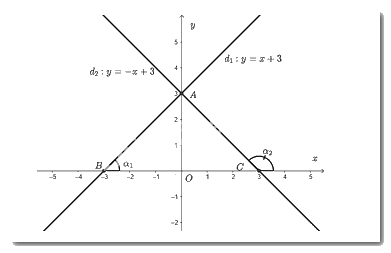
Từ đồ thị ta thấy giao điểm của hai đường thẳng là \(A\left( {0;3} \right)\).
Đường thẳng \({d_1}\) cắt trục \(Ox\) tại \(B\left( { - 3;0} \right)\).
Đường thẳng \({d_2}\) cắt trục \(Oy\) tại \(C\left( {3;0} \right)\).
b) Dùng thước đo góc để tìm góc tạo bởi \({d_1}\) và \({d_2}\) lần lượt với trục \(Ox\).
Phương pháp giải:
Đo góc
Lời giải chi tiết:
Gọi \({\alpha _1};{\alpha _2}\) lần lượt là 2 góc tạo bởi đường thẳng \({d_1};{d_2}\) với \(Ox\).
Dùng thước đo độ ta kiểm tra được\({\alpha _1} = 45^\circ ;{\alpha _2} = 135^\circ \).
c) Tính chu vi và diện tích của tam giác \(ABC\).
Phương pháp giải:
- Chu vi tam giác: \(C = a + b + c\) với \(a,b,c\) là ba cạnh tam giác.
- Diện tích tam giác: \(S = \dfrac{1}{2}a.{h_a}\) với \(a\) là độ dài đáy, \({h_a}\) là độ dài chiều cao tương ứng.
Lời giải chi tiết:
Vì \(Ox \bot Oy\) tại \(O\)nên tam giác \(AOB\) và tam giác \(AOC\) đều vuông tại \(O\).
Ta có: \(OA = 3;OB = 3;OC = 3\)
\(BC = OB + OC = 3 + 3 = 6\).
Áp dụng định lí Py – ta – go cho tam giác \(AOB\) ta có:
\(O{A^2} + O{B^2} = A{B^2}\)
\( \Leftrightarrow {3^2} + {3^2} = A{B^2}\)
\( \Leftrightarrow A{B^2} = 9 + 9 = 18\)
\( \Leftrightarrow AB = \sqrt {18} = 3\sqrt 2 \)
Áp dụng định lí Py – ta – go cho tam giác \(AOC\) ta có:
\(O{A^2} + O{C^2} = A{C^2}\)
\( \Leftrightarrow {3^2} + {3^2} = A{C^2}\)
\( \Leftrightarrow A{C^2} = 9 + 9 = 18\)
\( \Leftrightarrow AC = \sqrt {18} = 3\sqrt 2 \)
Chu vi tam giác \(ABC\) là:
\(C = AB + AC + BC = 3\sqrt 2 + 3\sqrt 2 + 6 = 6 + 6\sqrt 2 \) (đơn vị độ dài)
Vì \(Ox \bot Oy\) nên \(OA\) vuông góc với \(BC\) tại \(O\). Do đó, \(OA\) là đường cao tam giác \(ABC\) ứng với cạnh \(BC\).
Diện tích tam giác \(ABC\) là:
\(S = \dfrac{1}{2}OA.BC = \dfrac{1}{2}.3.6 = 9\) (đơn vị diện tích)
Vậy chu vi tam giác \(ABC\) là \(6 + 6\sqrt 2 \) đơn vị độ dài và diện tích tam giác \(ABC\) là 9 đơn vị diện tích.
a) Bằng cách vẽ hình, tìm tọa độ giao điểm \(A\) của hai đường thẳng nói trên và tìm các giao điểm \(B,C\) lần lượt của \({d_1}\) và \({d_2}\) với trục \(Ox\).
Phương pháp giải:
- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(M\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(N\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(M\) và \(N\), ta được đồ thị của hàm số \(y = ax + b\).
Lời giải chi tiết:
- Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
- Vẽ đồ thị hàm số \(y = - x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{{ - 1}} = 3\) ta được điểm \(C\left( {3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = - x + 3\) là đường thẳng đi qua hai điểm \(A\) và \(C\).
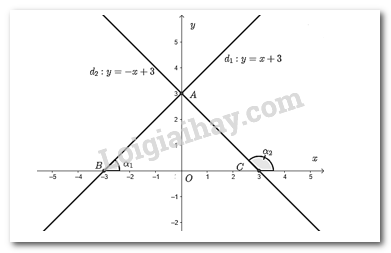
Từ đồ thị ta thấy giao điểm của hai đường thẳng là \(A\left( {0;3} \right)\).
Đường thẳng \({d_1}\) cắt trục \(Ox\) tại \(B\left( { - 3;0} \right)\).
Đường thẳng \({d_2}\) cắt trục \(Oy\) tại \(C\left( {3;0} \right)\).
Bài 19 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình học Toán 8, tập trung vào việc ôn tập chương 3: Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, rèn luyện kỹ năng phân tích và suy luận logic.
Bài 19 bao gồm các dạng bài tập sau:
Đề bài: Cho hàm số y = 2x + 3. Tính giá trị của y khi x = -1; x = 0; x = 1.
Giải:
Khi x = -1, ta có: y = 2*(-1) + 3 = -2 + 3 = 1.
Khi x = 0, ta có: y = 2*0 + 3 = 0 + 3 = 3.
Khi x = 1, ta có: y = 2*1 + 3 = 2 + 3 = 5.
Đề bài: Cho hàm số y = -x + 2. Tìm giá trị của x khi y = 0; y = 1; y = -1.
Giải:
Khi y = 0, ta có: 0 = -x + 2 => x = 2.
Khi y = 1, ta có: 1 = -x + 2 => x = 1.
Khi y = -1, ta có: -1 = -x + 2 => x = 3.
Đề bài: Lập bảng giá trị của hàm số y = 3x - 1 với x lần lượt nhận các giá trị -2; -1; 0; 1; 2.
Giải:
| x | y = 3x - 1 |
|---|---|
| -2 | 3*(-2) - 1 = -7 |
| -1 | 3*(-1) - 1 = -4 |
| 0 | 3*0 - 1 = -1 |
| 1 | 3*1 - 1 = 2 |
| 2 | 3*2 - 1 = 5 |
Để giải các bài tập về hàm số bậc nhất, các em cần nắm vững các kiến thức sau:
Bài 19 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.