Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 67 và 68 sách giáo khoa Toán 8 tập 2 – Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập. Hãy cùng bắt đầu nhé!
Cho tam giác
Video hướng dẫn giải
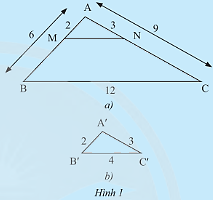
Cho tam giác \(ABC\) và tam giác \(A'B'C'\) có các kích thước như Hình 1. Trên cạnh \(AB\) và \(AC\) của tam giác \(ABC\) lần lượt lấy hai điểm \(M,N\) sao cho \(AM = 2cm,AN = 3cm\).
a) So sánh các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\).
b) Tính độ dài đoạn thẳng \(MN\).
c) Em có nhận xét gì về mối liên hệ giữa các tam giác \(ABC,AMN\) và \(A'B'C'\)?
Phương pháp giải:
- Ta tính tỉ số các đoạn thẳng.
- Sử dụng định lí Thales đảo.
- Hệ quả định lí Thales
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) và \(\Delta ABC\backsim\Delta A''B''C''\) thì \(\Delta A'B'C'\backsim\Delta A''B''C''\).
Lời giải chi tiết:
a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).
Video hướng dẫn giải
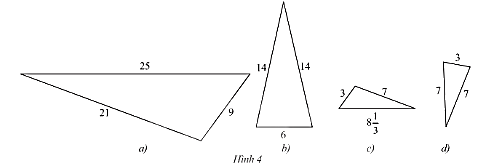
Tìm trong Hình 4 các cặp tam giác đồng dạng
Phương pháp giải:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Xét cặp tam giác thứ nhất: Hình a và Hình c.
Ta có: \(\frac{3}{9} = \frac{1}{3};\frac{7}{{21}} = \frac{1}{3};\frac{{8\frac{1}{3}}}{{25}} = \frac{1}{3}\).
Do đó, tam giác ở Hình a và Hình c đồng dạng với nhau.
Xét cặp tam giác thứ hai: Hình b và Hình d.
Ta có: \(\frac{7}{{14}} = \frac{1}{2};\frac{7}{{14}} = \frac{1}{2};\frac{3}{6} = \frac{1}{2}\).
Do đó, tam giác ở Hình b và Hình d đồng dạng với nhau.
Video hướng dẫn giải
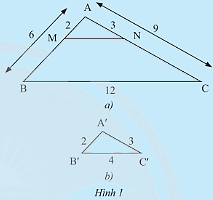
Cho tam giác \(ABC\) và tam giác \(A'B'C'\) có các kích thước như Hình 1. Trên cạnh \(AB\) và \(AC\) của tam giác \(ABC\) lần lượt lấy hai điểm \(M,N\) sao cho \(AM = 2cm,AN = 3cm\).
a) So sánh các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\).
b) Tính độ dài đoạn thẳng \(MN\).
c) Em có nhận xét gì về mối liên hệ giữa các tam giác \(ABC,AMN\) và \(A'B'C'\)?
Phương pháp giải:
- Ta tính tỉ số các đoạn thẳng.
- Sử dụng định lí Thales đảo.
- Hệ quả định lí Thales
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) và \(\Delta ABC\backsim\Delta A''B''C''\) thì \(\Delta A'B'C'\backsim\Delta A''B''C''\).
Lời giải chi tiết:
a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).
Video hướng dẫn giải
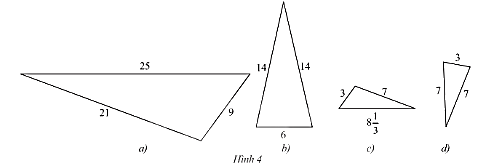
Tìm trong Hình 4 các cặp tam giác đồng dạng
Phương pháp giải:
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
Lời giải chi tiết:
Xét cặp tam giác thứ nhất: Hình a và Hình c.
Ta có: \(\frac{3}{9} = \frac{1}{3};\frac{7}{{21}} = \frac{1}{3};\frac{{8\frac{1}{3}}}{{25}} = \frac{1}{3}\).
Do đó, tam giác ở Hình a và Hình c đồng dạng với nhau.
Xét cặp tam giác thứ hai: Hình b và Hình d.
Ta có: \(\frac{7}{{14}} = \frac{1}{2};\frac{7}{{14}} = \frac{1}{2};\frac{3}{6} = \frac{1}{2}\).
Do đó, tam giác ở Hình b và Hình d đồng dạng với nhau.
Mục 1 của chương trình Toán 8 tập 2 – Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về các tứ giác đặc biệt: hình bình hành, hình chữ nhật, hình thoi, hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và các ứng dụng của các tứ giác này là vô cùng quan trọng, không chỉ cho việc giải các bài tập trong SGK mà còn là nền tảng cho các kiến thức toán học ở các lớp trên.
Trang 67 và 68 SGK Toán 8 tập 2 – Chân trời sáng tạo bao gồm các bài tập vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến các tứ giác đặc biệt. Các bài tập này thường yêu cầu học sinh:
Bài 1 thường yêu cầu học sinh nhắc lại các tính chất của hình bình hành, dấu hiệu nhận biết hình bình hành và các ứng dụng của hình bình hành trong thực tế. Để giải bài này, học sinh cần nắm vững định nghĩa, tính chất và dấu hiệu nhận biết hình bình hành.
Bài 2 tập trung vào việc ôn tập về hình chữ nhật, bao gồm các tính chất, dấu hiệu nhận biết và các ứng dụng của hình chữ nhật. Học sinh cần hiểu rõ mối quan hệ giữa hình chữ nhật và hình bình hành, cũng như các công thức tính diện tích và chu vi của hình chữ nhật.
Bài 3 yêu cầu học sinh ôn tập về hình thoi, bao gồm các tính chất, dấu hiệu nhận biết và các ứng dụng của hình thoi. Học sinh cần nắm vững mối quan hệ giữa hình thoi và hình bình hành, cũng như các công thức tính diện tích của hình thoi.
Bài 4 tập trung vào việc ôn tập về hình vuông, bao gồm các tính chất, dấu hiệu nhận biết và các ứng dụng của hình vuông. Học sinh cần hiểu rõ mối quan hệ giữa hình vuông và các hình bình hành, hình chữ nhật, hình thoi khác, cũng như các công thức tính diện tích và chu vi của hình vuông.
Để giải các bài tập trong mục 1 trang 67, 68 SGK Toán 8 tập 2 – Chân trời sáng tạo một cách hiệu quả, học sinh nên:
Bài tập: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng AF = 2FC.
Lời giải:
Xét tam giác ABC, có E là trung điểm của AB và F là giao điểm của DE và AC. Áp dụng định lý Menelaus cho tam giác ABC với đường thẳng DE, ta có:
(AE/EB) * (BD/DC) * (CF/FA) = 1
Vì E là trung điểm của AB nên AE/EB = 1. Vì ABCD là hình bình hành nên BD/DC = 1. Do đó:
1 * 1 * (CF/FA) = 1 => CF/FA = 1 => AF = 2FC (đpcm)
Hãy dành thời gian ôn tập lý thuyết và làm nhiều bài tập để nắm vững kiến thức về các tứ giác đặc biệt. Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn. Chúc các em học tập tốt!