Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 23 và 24 sách giáo khoa Toán 8 tập 2 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
a) Trong mặt phẳng tọa độ (Oxy), cho đường thẳng
Video hướng dẫn giải
Tìm hệ số góc của các đường thẳng sau đây:
a) \(y = - 5x - 5\);
b) \(y = \sqrt 3 x + 3\);
c) \(y = \sqrt {11} x + \sqrt 7 \)
Phương pháp giải:
Hệ số \(a\) là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\).
Lời giải chi tiết:
a) Đường thẳng \(y = - 5x - 5\) có hệ số góc là \(a = - 5\).
b) Đường thẳng \(y = \sqrt 3 x + 3\) có hệ số góc là \(a = \sqrt 3 \).
c) Đường thẳng \(y = \sqrt {11} x + \sqrt 7 \) có hệ số góc là \(a = \sqrt {11} \).
Video hướng dẫn giải
Trong các đường thẳng sau, đường thẳng nào tạo với \(Ox\) một góc nhọn, đường thẳng nào tạo với \(Ox\) một góc tù?
a) \(y = 3x + 6\);
b) \(y = - 4x + 1\);
c) \(y = - 3x - 6\)
Phương pháp giải:
- Khi hệ số \(a\) dương \(\left( {a > 0} \right)\) thì góc \(\alpha \) tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\) là góc nhọn.
- Khi hệ số \(a\) âm \(\left( {a < 0} \right)\) thì góc \(\alpha \) tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\) là góc tù.
Lời giải chi tiết:
a) Đường thẳng \(y = 3x + 6\) có hệ số góc là \(a = 3 > 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là góc nhọn.
b) Đường thẳng \(y = - 4x + 1\) có hệ số góc là \(a = - 4 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.
c) Đường thẳng \(y = - 3x - 6\) có hệ số góc là \(a = - 3 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.
Video hướng dẫn giải
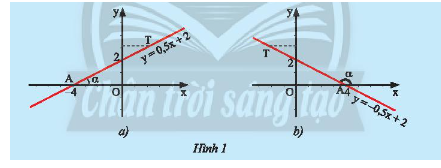
a) Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) cắt \(Ox\) tại điểm \(A\) và \(T\) là một điểm trên đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có tung độ dương (Hình 1).
Ta gọi \(\alpha = \widehat {xAT}\) là góc tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\).
Hãy nêu nhận xét của em về số đo của góc \(\alpha \) và hệ số \(a\) trong hai trường hợp dưới đây.
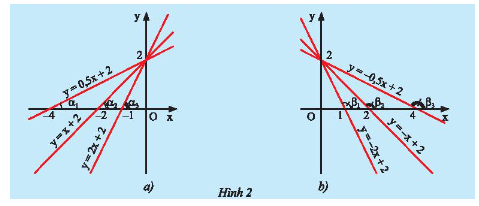
b) Hãy so sánh các hệ số \(a\) của các đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) trong mỗi hình ở Hình 2 và so sánh các góc \(\alpha \) hoặc các góc \(\beta \) tạo bởi các đường thẳng đó với trục \(Ox\).
Phương pháp giải:
- Góc vuông là góc có số đo bằng \(90^\circ \).
- Góc nhọn là góc có số đo nhỏ hơn \(90^\circ \).
- Góc tù là góc có số đo lớn hơn \(90^\circ \).
- Góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó.
Lời giải chi tiết:
a)
- Ở hình 1a là đồ thị của hàm số \(y = 0,5x + 2\) hệ số \(a = 0,5 > 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc nhọn.
- Ở hình 1b là đồ thị của hàm số \(y = - 0,5x + 2\) hệ số \(a = - 0,5 < 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc tù.
b)
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).
Video hướng dẫn giải
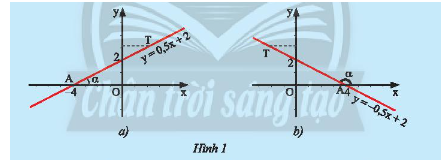
a) Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) cắt \(Ox\) tại điểm \(A\) và \(T\) là một điểm trên đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có tung độ dương (Hình 1).
Ta gọi \(\alpha = \widehat {xAT}\) là góc tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\).
Hãy nêu nhận xét của em về số đo của góc \(\alpha \) và hệ số \(a\) trong hai trường hợp dưới đây.
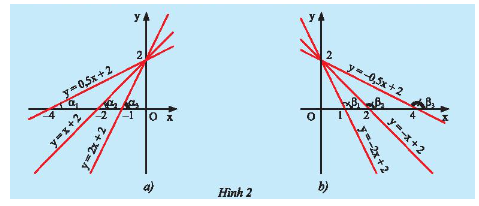
b) Hãy so sánh các hệ số \(a\) của các đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) trong mỗi hình ở Hình 2 và so sánh các góc \(\alpha \) hoặc các góc \(\beta \) tạo bởi các đường thẳng đó với trục \(Ox\).
Phương pháp giải:
- Góc vuông là góc có số đo bằng \(90^\circ \).
- Góc nhọn là góc có số đo nhỏ hơn \(90^\circ \).
- Góc tù là góc có số đo lớn hơn \(90^\circ \).
- Góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó.
Lời giải chi tiết:
a)
- Ở hình 1a là đồ thị của hàm số \(y = 0,5x + 2\) hệ số \(a = 0,5 > 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc nhọn.
- Ở hình 1b là đồ thị của hàm số \(y = - 0,5x + 2\) hệ số \(a = - 0,5 < 0\); Dùng thước đo độ kiểm tra ta thấy góc \(\alpha \) là góc tù.
b)
- Ở hình 2a là đồ thị của 3 hàm số \(y = 0,5x + 2;y = x + 2;y = 2x + 2\).
Ta có: \({a_1} = 0,5;{a_2} = 1;{a_3} = 2\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\alpha _1} < {\alpha _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\alpha _2} < {\alpha _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\alpha _1} < {\alpha _2} < {\alpha _3}\).
- Ở hình 2b là đồ thị của 3 hàm số \(y = - 2x + 2;y = - x + 2;y = - 0,5x + 2\).
Ta có: \({a_1} = - 2;{a_2} = - 1;{a_3} = - 0,5\) nên \({a_1} < {a_2} < {a_3}\).
Ta có: \({\beta _1} < {\beta _2}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
\({\beta _2} < {\beta _3}\) (góc ngoài của tam giác luôn lớn hơn góc trong không kề với nó).
Do đó, \({\beta _1} < {\beta _2} < {\beta _3}\).
Video hướng dẫn giải
Tìm hệ số góc của các đường thẳng sau đây:
a) \(y = - 5x - 5\);
b) \(y = \sqrt 3 x + 3\);
c) \(y = \sqrt {11} x + \sqrt 7 \)
Phương pháp giải:
Hệ số \(a\) là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\).
Lời giải chi tiết:
a) Đường thẳng \(y = - 5x - 5\) có hệ số góc là \(a = - 5\).
b) Đường thẳng \(y = \sqrt 3 x + 3\) có hệ số góc là \(a = \sqrt 3 \).
c) Đường thẳng \(y = \sqrt {11} x + \sqrt 7 \) có hệ số góc là \(a = \sqrt {11} \).
Video hướng dẫn giải
Trong các đường thẳng sau, đường thẳng nào tạo với \(Ox\) một góc nhọn, đường thẳng nào tạo với \(Ox\) một góc tù?
a) \(y = 3x + 6\);
b) \(y = - 4x + 1\);
c) \(y = - 3x - 6\)
Phương pháp giải:
- Khi hệ số \(a\) dương \(\left( {a > 0} \right)\) thì góc \(\alpha \) tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\) là góc nhọn.
- Khi hệ số \(a\) âm \(\left( {a < 0} \right)\) thì góc \(\alpha \) tạo bởi đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và trục \(Ox\) là góc tù.
Lời giải chi tiết:
a) Đường thẳng \(y = 3x + 6\) có hệ số góc là \(a = 3 > 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là góc nhọn.
b) Đường thẳng \(y = - 4x + 1\) có hệ số góc là \(a = - 4 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.
c) Đường thẳng \(y = - 3x - 6\) có hệ số góc là \(a = - 3 < 0\) nên góc tạo bởi đường thẳng và trục \(Ox\) là tù.
Mục 1 của chương trình Toán 8 tập 2 Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về các phép biến đổi đơn giản với đa thức. Các bài tập trong mục này giúp học sinh củng cố các kỹ năng như thu gọn đa thức, cộng trừ đa thức, nhân đa thức và chia đa thức. Việc nắm vững những kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài 1 yêu cầu học sinh thu gọn các đa thức đã cho. Để thu gọn một đa thức, ta cần thực hiện các bước sau:
Ví dụ, để thu gọn đa thức 3x2 + 2x - x2 + 5x - 3, ta thực hiện như sau:
Bài 2 yêu cầu học sinh thực hiện các phép cộng và trừ đa thức. Để cộng hoặc trừ hai đa thức, ta thực hiện các bước sau:
Ví dụ, để cộng hai đa thức A = 2x2 + 3x - 1 và B = -x2 + 5x + 2, ta thực hiện như sau:
Bài 3 yêu cầu học sinh thực hiện phép nhân đa thức. Để nhân hai đa thức, ta sử dụng quy tắc phân phối:
A(B + C) = AB + AC
Ví dụ, để nhân hai đa thức A = 2x + 1 và B = x - 3, ta thực hiện như sau:
Bài 4 yêu cầu học sinh thực hiện phép chia đa thức. Phép chia đa thức có thể được thực hiện bằng phương pháp chia trực tiếp hoặc phương pháp đặt ẩn phụ. Tùy thuộc vào độ phức tạp của đa thức, ta có thể lựa chọn phương pháp phù hợp.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 23, 24 SGK Toán 8 tập 2 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!