Bài 3 trang 54 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 54 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho biết cạnh mỗi ô vuông bằng
Đề bài
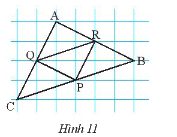
Cho biết cạnh mỗi ô vuông bằng \(1cm\). Tính độ dài các đoạn \(PQ,PR,RQ,AB,BC,CA\) trong Hình 11.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm của tam giác.
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Định lí Py – ta – go cho tam giác vuông.
Lời giải chi tiết
Đoạn thẳng \(AB\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\).
Áp dụng định lí Py – ta – go ta được:
\(A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \) suy ra \(AB = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(AC\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\).
Áp dụng định lí Py – ta – go ta được:
\(A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \) suy ra \(AC = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(BC\) là đường chéo của hình chữ nhật với chiều dài là \(6cm;\) chiều rộng là \(2cm\).
Áp dụng định lí Py – ta – go ta được:
\(B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \) suy ra \(BC = \sqrt {40} = 2\sqrt {10} \)
Từ hình vẽ ta thấy:
\(Q\) là trung điểm của \(AC\);
\(R\) là trung điểm của \(AB\);
\(P\) là trung điểm của \(BC\).
- Vì \(Q\) là trung điểm của \(AC\); \(R\) là trung điểm của \(AB\) nên \(QR\) là đường trung bình của tam giác \(ABC \) suy ra \(QR = \frac{1}{2}BC\) (tính chất đường trung bình)
Do đó \(QR = \frac{1}{2}.2\sqrt {10} = \sqrt {10} \left( {cm} \right)\).
- Vì \(Q\) là trung điểm của \(AC\); \(P\) là trung điểm của \(BC\) nên \(QP\) là đường trung bình của tam giác \(ABC \) suy ra \(QP = \frac{1}{2}AB\) (tính chất đường trung bình)
Do đó \(QP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
- Vì \(R\) là trung điểm của \(AB\); \(P\) là trung điểm của \(BC\) nên \(RP\) là đường trung bình của tam giác \(ABC \) suy ra \(RP = \frac{1}{2}AC\) (tính chất đường trung bình)
Do đó \(RP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
Bài 3 trang 54 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về phân thức đại số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như phân thức, điều kiện xác định của phân thức, và các phép toán trên phân thức (cộng, trừ, nhân, chia).
Bài 3 thường yêu cầu học sinh thực hiện một trong các nhiệm vụ sau:
Để giải bài 3 trang 54 SGK Toán 8 tập 2, chúng ta sẽ đi qua từng bước sau:
Giả sử bài tập yêu cầu chúng ta rút gọn phân thức A = (x2 - 1) / (x + 1). Ta thực hiện như sau:
Vậy, phân thức A sau khi rút gọn là x - 1.
Khi giải bài tập về phân thức, học sinh cần chú ý các điểm sau:
Việc giải bài 3 trang 54 SGK Toán 8 tập 2 không chỉ giúp học sinh nắm vững kiến thức về phân thức đại số mà còn có ứng dụng thực tế trong nhiều lĩnh vực khác nhau, chẳng hạn như:
Bài 3 trang 54 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về phân thức đại số. Bằng cách nắm vững các khái niệm cơ bản và áp dụng các bước giải chi tiết, học sinh có thể tự tin giải quyết bài tập này một cách hiệu quả. Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Phân thức | Biểu thức có dạng P/Q, trong đó P và Q là các đa thức, và Q khác 0. |
| Điều kiện xác định | Các giá trị của biến sao cho mẫu số của phân thức khác 0. |
| Rút gọn phân thức | Chia cả tử số và mẫu số cho nhân tử chung. |