Bài 8 trang 89 SGK Toán 8 tập 1 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 89 SGK Toán 8 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hình bình hành
Đề bài
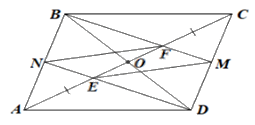
Cho hình bình hành \(ABCD\). Các điểm \(E\), \(F\) thuộc đường chéo \(AC\) sao cho \(AE = EF = FC\). Gọi \(M\) là trung điểm của \(BF\) và \(CD\), \(N\) là giao điểm của \(DE\) và \(AB\). Chứng minh rằng:
a) \(M\), \(N\) theo thứ tự là trung điểm của \(CD\), \(AB\)
b) \(EMFN\) là hình bình hành
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng tính chất của hình bình hành
Áp dụng dấu hiệu nhận biết của hình bình hành
Lời giải chi tiết
a) Ta có:
\(AE = EF = FC\) nên \(AE = EF = FC = \frac{1}{3}AC\) (1)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\) hay \(OA = OC = \frac{1}{2}AC\) và \(AC = 2OA = 2OC\) (2)
Từ (1) và (2) suy ra \(AE = EF = FC = \frac{2}{3}OA = \frac{2}{3}OC\).
Xét \(\Delta BCD\) có \(CO\) là trung tuyến và \(CF = \frac{2}{3}CO\) (cmt)
Suy ra \(F\) là trọng tâm của \(\Delta BCD\)
Suy ra \(BM\) là đường trung tuyến của \(\Delta BCD\)
Suy ra \(M\) là trung điểm của \(CD\)
Xét \(\Delta ABD\) có \(AO\) là trung tuyến và \(AE = \frac{2}{3}AO\) (cmt)
Suy ra \(E\) là trọng tâm của \(\Delta ABD\)
Suy ra \(DN\) là đường trung tuyến của \(\Delta ABD\)
Suy ra \(N\) là trung điểm của \(AB\)
b) Do M là trung điểm của CD (câu a) nên \(MC = MD = \frac{1}{2}CD\).
N là trung điểm của AB (câu a) nên \(NB = NA = \frac{1}{2}AB\).
Mà AB = CD và AB // CD (do ABCD là hình bình hành)
Suy ra NB = MD và NB // MD.
Xét tứ giác BMDN có NB = MD và NB // MD
Do đó BMDN là hình bình hành.
Suy ra BM // DN và BM = DN.
Ta có E là trọng tâm của \(\Delta\)ABD nên \(EN = \frac{1}{3}DN\).
F là trọng tâm của \(\Delta\)BCD nên \(FM = \frac{1}{3}BM\).
Mà DN = BM (chứng minh trên) nên EN = FM.
Xét tứ giác EMFN có EN = FM và EN // FM (do BM // DN)
Suy ra EMFN là hình bình hành.
Bài 8 trang 89 SGK Toán 8 tập 1 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về các phép biến đổi đại số, đặc biệt là các quy tắc cộng, trừ, nhân, chia đa thức để giải quyết bài toán. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như đơn thức, đa thức, bậc của đa thức, hệ số của đa thức, và các phép toán trên đa thức.
Trước khi bắt đầu giải bài tập, học sinh nên đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và các dữ kiện đã cho. Sau đó, học sinh cần phân tích bài toán để tìm ra hướng giải quyết phù hợp. Trong bài 8 trang 89, học sinh thường cần thực hiện các bước sau:
Dưới đây là lời giải chi tiết bài 8 trang 89 SGK Toán 8 tập 1 – Chân trời sáng tạo. Lưu ý rằng, tùy thuộc vào từng dạng bài tập cụ thể, phương pháp giải có thể khác nhau. Tuy nhiên, các bước phân tích và giải quyết bài toán như đã trình bày ở trên vẫn là những bước cơ bản và quan trọng.
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng từng bước, và kết quả cuối cùng. Ví dụ:)
Bài 8a: Thực hiện phép tính: (x + 2)(x - 2)
Lời giải:
(x + 2)(x - 2) = x2 - 22 = x2 - 4
Bài 8b: Rút gọn biểu thức: 3x(x - 1) + 2(x - 1)
Lời giải:
3x(x - 1) + 2(x - 1) = (3x + 2)(x - 1) = 3x2 - 3x + 2x - 2 = 3x2 - x - 2
Ngoài bài 8 trang 89, SGK Toán 8 tập 1 – Chân trời sáng tạo còn có nhiều bài tập khác liên quan đến các phép biến đổi đại số. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về các phép biến đổi đại số, các công thức phân tích đa thức thành nhân tử, và các quy tắc thực hiện các phép toán trên đa thức.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh nên làm thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, học sinh cũng có thể tham gia các khóa học toán online hoặc tìm kiếm sự giúp đỡ của giáo viên và bạn bè.
Bài 8 trang 89 SGK Toán 8 tập 1 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bằng cách nắm vững kiến thức cơ bản, phân tích bài toán một cách cẩn thận, và áp dụng các phương pháp giải phù hợp, học sinh có thể giải quyết bài tập này một cách hiệu quả và tự tin hơn trong quá trình học tập.