Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 84, 85, 86 sách giáo khoa Toán 8 tập 1 – Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Cho tứ giác
Video hướng dẫn giải
Tìm bốn ví dụ về hình vuông trong thực tế
Phương pháp giải:
Sử dụng định nghĩa hình vuông
Lời giải chi tiết:
Mặt bàn hình vuông
Ô cửa sổ hình vuông
Hộp phấn
Viên gạch
Video hướng dẫn giải
Cho hình thoi \(ABCD\). Hãy chứng tỏ:
a) Nếu \(\widehat {BAD}\) là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {BAD}\) là góc vuông
Phương pháp giải:
Áp dụng tính chất của hình thoi, hình bình hành
Lời giải chi tiết:
a)
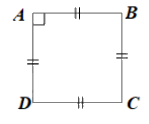
\(ABCD\) là hình thoi nên cũng là hình bình hành.
Suy ra:
\(AB = BC = CD = DA\);
\(\widehat A = \widehat C;\;\widehat B = \widehat D\)
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra: \(\widehat A + \widehat B = \widehat C + \widehat D = 180^\circ \)
Mà \(\widehat {BAD}\) là góc vuông
Suy ra \(\widehat {BCD} = 90^\circ \); \(\widehat B = 90^\circ ;\;\widehat D = 90^\circ \)
b) Nếu \(AC = BD\) thì \(ABCD\) là hình chữ nhật
Khi đó \(\widehat {BAD}\) là góc vuông
Video hướng dẫn giải
Cho tứ giác \(ABCD\) có bốn góc bằng nhau và có bốn cạnh bằng nhau. Hãy chứng tỏ \(ABCD\) vừa là hình thoi vừa là hình thoi vừa là hình chữ nhật.
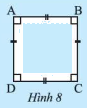
Phương pháp giải:
Áp dụng dấu hiệu nhận biết hình thoi và hình chữ nhật
Lời giải chi tiết:
Xét tứ giác \(ABCD\) có bốn góc bằng nhau: \(\widehat A = \widehat B = \widehat C = \widehat D\) mà \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra \(\widehat A = \widehat B = \widehat C = \widehat D = \frac{{360^\circ }}{4} = 90^\circ \)
Suy ra \(ABCD\) là hình chữ nhật
Xét tứ giác \(ABCD\) có bốn cạnh \(AB = BC = CD = DA\) nên là hình thoi
Vậy \(ABCD\) vừa là hình thoi vừa là hình chữ nhật
Video hướng dẫn giải
Cho hình vuông \(MNPQ\). Chứng minh \(MNPQ\) vừa là hình chữ nhật vừa là hình thoi.
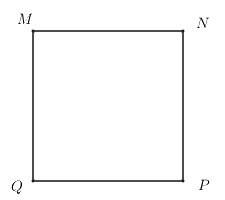
Phương pháp giải:
Sử dụng định nghĩa hình vuông, dấu hiệu nhận biết của hình thoi và hình chữ nhật
Lời giải chi tiết:
Vì \(MNPQ\) là hình vuông (gt)
Suy ra \(MN = NP = PQ = QM\) nên \(MNPQ\) là hình thoi
Và \(\widehat M = \widehat N = \widehat P = \widehat Q = 90^\circ \) nên \(MNPQ\) là hình chữ nhật
Vậy\(MNPQ\) vừa là hình thoi vừa là hình chữ nhật
Video hướng dẫn giải
Trong Hình 12, cho biết \(ABCD\) là một hình vuông. Chứng minh rằng:
a) Tứ giác \(EFGH\) có ba góc vuông
b) \(HE = HG\)
c) Tứ giác \(EFGH\) là một hình vuông
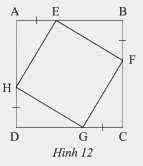
Phương pháp giải:
Áp dụng tính chất của hình vuông, hai tam giác bằng nhau
Lời giải chi tiết:
a) Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\); \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \)
Mà \(AE = BF = CG = HD\) (gt) suy ra \(BE = CF = DG = AH\)
Xét \(\Delta AEH\) và \(\Delta DHG\) ta có:
\(\widehat {\rm{A}} = \widehat {\rm{D}} = 90\)
\(AE = GH\) (gt)
\(AH = DG\) (gt)
Suy ra \(\Delta AEH = \Delta DHG\) (c-g-c)
Suy ra \(\widehat {{\rm{AEH}}} = \widehat {{\rm{DHG}}}\) (hai góc tương ứng)
Mà \(\widehat {AEH} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {DHG} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {EHG} = 90^\circ \)
Chứng minh tương tự ta được \(\widehat {HGF} = 90^\circ ;\;\widehat {GFE} = 90^\circ \)
Vậy tứ giác \(EFGH\) có ba góc vuông.
b) Vì \(\Delta AEH = \Delta DHG\) (cmt)
Suy ra \(HE = HG\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông
c) chứng minh tương tự câu b ta có: \(HE = EF\); \(HE = FG\)
Khi đó \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi (3)
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (4)
Từ (3) và (4) suy ra \(EFGH\) là hình vuông
Video hướng dẫn giải
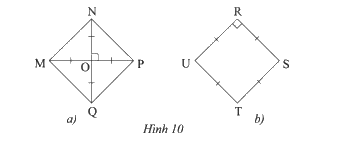
Tìm hình vuông trong hai hình sau:
Phương pháp giải:
Áp dụng định nghĩa hình vuông để tìm hình vuông trong hình vẽ
Lời giải chi tiết:
a) Xét tứ giác \(MNPQ\) có hai đường chéo \(MP\) và \(NQ\) cắt nhau tại trung điểm \(O\)
Suy ra \(MNPQ\) là hình bình hành
Mà hai đường chéo \(MP\) và \(NQ\) vuông góc
Suy ra \(MNPQ\) là hình thoi
Mà \(MP = 2OM\); \(NQ = 2ON\) và \(OM = ON\) (gt)
Suy ra \(MP = NQ\)
Suy ra \(MNPQ\) là hình vuông
b) Tứ giác \(URST\) có:
\(UR = RS = ST = TU\) (gt)
Suy ra \(URST\) là hình thoi, hình bình hành
Mà \(\widehat {{\rm{UR}}S} = 90^\circ \) (gt)
Suy ra \(URST\) là hình chữ nhật
Do đó \(URST\) có 4 góc vuông
Mà \(URST\) có 4 cạnh bằng nhau
Suy ra \(URST\) là hình vuông
Video hướng dẫn giải
Bạn Nam kiểm tra mặt kính của chiếc đồng hồ để bàn và nhận thấy có ba góc vuông và hai cạnh kề bằng nhau (Hình 13). Hãy cho biết mặt kính đồng hồ có hình gì?

Phương pháp giải:
Áp dụng dấu hiệu nhận biết của hình vuông
Lời giải chi tiết:
Mặt kính đồng hồ có ba góc vuông nên là hình chữ nhật
Mà mặt kính có hai cạnh kề bằng nhau
Suy ra mặt kính đồng hồ là hình vuông
Video hướng dẫn giải
Cho hình chữ nhật \(ABCD\). Giải thích tại sao \(ABCD\) là hình vuông trong mỗi trường hợp sau:
Trường hợp 1: \(AB = BC\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là đường phân giác của góc \(BAD\)
Phương pháp giải:
Áp dụng tính chất của hình chữ nhật, định nghĩa hình vuông
Lời giải chi tiết:
\(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\) (3)
\(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \) (1)
TH1:
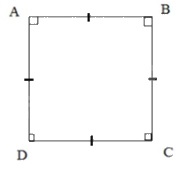
Nếu \(AB = BC\) (gt) thì \(AB = BC = CD = DA\) (2)
Từ (1), (2) suy ra \(ABCD\) là hình vuông
TH2:

Nếu \(AC\) vuông góc với \(BD\)
Mà \(ABCD\) cũng là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (4)
Từ (1) và (4) suy ra \(ABCD\) là hình vuông
TH3:

\(AC\) là phân giác của góc \(BAD\)
Mà \(ABCD\) là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (5)
Từ (1) và (5) suy ra \(ABCD\) là hình vuông
Video hướng dẫn giải
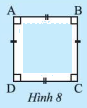
Cho tứ giác \(ABCD\) có bốn góc bằng nhau và có bốn cạnh bằng nhau. Hãy chứng tỏ \(ABCD\) vừa là hình thoi vừa là hình thoi vừa là hình chữ nhật.
Phương pháp giải:
Áp dụng dấu hiệu nhận biết hình thoi và hình chữ nhật
Lời giải chi tiết:
Xét tứ giác \(ABCD\) có bốn góc bằng nhau: \(\widehat A = \widehat B = \widehat C = \widehat D\) mà \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra \(\widehat A = \widehat B = \widehat C = \widehat D = \frac{{360^\circ }}{4} = 90^\circ \)
Suy ra \(ABCD\) là hình chữ nhật
Xét tứ giác \(ABCD\) có bốn cạnh \(AB = BC = CD = DA\) nên là hình thoi
Vậy \(ABCD\) vừa là hình thoi vừa là hình chữ nhật
Video hướng dẫn giải
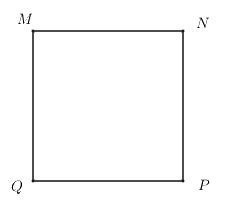
Cho hình vuông \(MNPQ\). Chứng minh \(MNPQ\) vừa là hình chữ nhật vừa là hình thoi.
Phương pháp giải:
Sử dụng định nghĩa hình vuông, dấu hiệu nhận biết của hình thoi và hình chữ nhật
Lời giải chi tiết:
Vì \(MNPQ\) là hình vuông (gt)
Suy ra \(MN = NP = PQ = QM\) nên \(MNPQ\) là hình thoi
Và \(\widehat M = \widehat N = \widehat P = \widehat Q = 90^\circ \) nên \(MNPQ\) là hình chữ nhật
Vậy\(MNPQ\) vừa là hình thoi vừa là hình chữ nhật
Video hướng dẫn giải
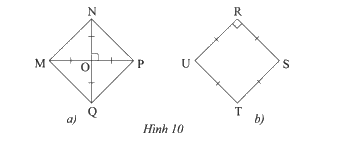
Tìm hình vuông trong hai hình sau:
Phương pháp giải:
Áp dụng định nghĩa hình vuông để tìm hình vuông trong hình vẽ
Lời giải chi tiết:
a) Xét tứ giác \(MNPQ\) có hai đường chéo \(MP\) và \(NQ\) cắt nhau tại trung điểm \(O\)
Suy ra \(MNPQ\) là hình bình hành
Mà hai đường chéo \(MP\) và \(NQ\) vuông góc
Suy ra \(MNPQ\) là hình thoi
Mà \(MP = 2OM\); \(NQ = 2ON\) và \(OM = ON\) (gt)
Suy ra \(MP = NQ\)
Suy ra \(MNPQ\) là hình vuông
b) Tứ giác \(URST\) có:
\(UR = RS = ST = TU\) (gt)
Suy ra \(URST\) là hình thoi, hình bình hành
Mà \(\widehat {{\rm{UR}}S} = 90^\circ \) (gt)
Suy ra \(URST\) là hình chữ nhật
Do đó \(URST\) có 4 góc vuông
Mà \(URST\) có 4 cạnh bằng nhau
Suy ra \(URST\) là hình vuông
Video hướng dẫn giải
Tìm bốn ví dụ về hình vuông trong thực tế
Phương pháp giải:
Sử dụng định nghĩa hình vuông
Lời giải chi tiết:
Mặt bàn hình vuông
Ô cửa sổ hình vuông
Hộp phấn
Viên gạch
Video hướng dẫn giải
Cho hình chữ nhật \(ABCD\). Giải thích tại sao \(ABCD\) là hình vuông trong mỗi trường hợp sau:
Trường hợp 1: \(AB = BC\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là đường phân giác của góc \(BAD\)
Phương pháp giải:
Áp dụng tính chất của hình chữ nhật, định nghĩa hình vuông
Lời giải chi tiết:
\(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\) (3)
\(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \) (1)
TH1:
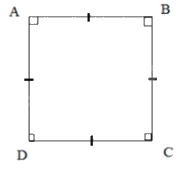
Nếu \(AB = BC\) (gt) thì \(AB = BC = CD = DA\) (2)
Từ (1), (2) suy ra \(ABCD\) là hình vuông
TH2:
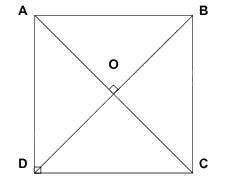
Nếu \(AC\) vuông góc với \(BD\)
Mà \(ABCD\) cũng là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (4)
Từ (1) và (4) suy ra \(ABCD\) là hình vuông
TH3:
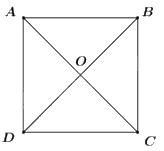
\(AC\) là phân giác của góc \(BAD\)
Mà \(ABCD\) là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (5)
Từ (1) và (5) suy ra \(ABCD\) là hình vuông
Video hướng dẫn giải
Cho hình thoi \(ABCD\). Hãy chứng tỏ:
a) Nếu \(\widehat {BAD}\) là góc vuông thì ba góc còn lại của hình thoi cũng là góc vuông.
b) Nếu \(AC = BD\) thì \(\widehat {BAD}\) là góc vuông
Phương pháp giải:
Áp dụng tính chất của hình thoi, hình bình hành
Lời giải chi tiết:
a)
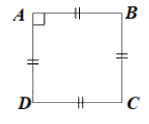
\(ABCD\) là hình thoi nên cũng là hình bình hành.
Suy ra:
\(AB = BC = CD = DA\);
\(\widehat A = \widehat C;\;\widehat B = \widehat D\)
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Suy ra: \(\widehat A + \widehat B = \widehat C + \widehat D = 180^\circ \)
Mà \(\widehat {BAD}\) là góc vuông
Suy ra \(\widehat {BCD} = 90^\circ \); \(\widehat B = 90^\circ ;\;\widehat D = 90^\circ \)
b) Nếu \(AC = BD\) thì \(ABCD\) là hình chữ nhật
Khi đó \(\widehat {BAD}\) là góc vuông
Video hướng dẫn giải
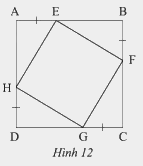
Trong Hình 12, cho biết \(ABCD\) là một hình vuông. Chứng minh rằng:
a) Tứ giác \(EFGH\) có ba góc vuông
b) \(HE = HG\)
c) Tứ giác \(EFGH\) là một hình vuông
Phương pháp giải:
Áp dụng tính chất của hình vuông, hai tam giác bằng nhau
Lời giải chi tiết:
a) Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\); \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \)
Mà \(AE = BF = CG = HD\) (gt) suy ra \(BE = CF = DG = AH\)
Xét \(\Delta AEH\) và \(\Delta DHG\) ta có:
\(\widehat {\rm{A}} = \widehat {\rm{D}} = 90\)
\(AE = GH\) (gt)
\(AH = DG\) (gt)
Suy ra \(\Delta AEH = \Delta DHG\) (c-g-c)
Suy ra \(\widehat {{\rm{AEH}}} = \widehat {{\rm{DHG}}}\) (hai góc tương ứng)
Mà \(\widehat {AEH} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {DHG} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {EHG} = 90^\circ \)
Chứng minh tương tự ta được \(\widehat {HGF} = 90^\circ ;\;\widehat {GFE} = 90^\circ \)
Vậy tứ giác \(EFGH\) có ba góc vuông.
b) Vì \(\Delta AEH = \Delta DHG\) (cmt)
Suy ra \(HE = HG\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông
c) chứng minh tương tự câu b ta có: \(HE = EF\); \(HE = FG\)
Khi đó \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi (3)
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (4)
Từ (3) và (4) suy ra \(EFGH\) là hình vuông
Video hướng dẫn giải
Bạn Nam kiểm tra mặt kính của chiếc đồng hồ để bàn và nhận thấy có ba góc vuông và hai cạnh kề bằng nhau (Hình 13). Hãy cho biết mặt kính đồng hồ có hình gì?

Phương pháp giải:
Áp dụng dấu hiệu nhận biết của hình vuông
Lời giải chi tiết:
Mặt kính đồng hồ có ba góc vuông nên là hình chữ nhật
Mà mặt kính có hai cạnh kề bằng nhau
Suy ra mặt kính đồng hồ là hình vuông
Mục 2 của chương trình Toán 8 tập 1 – Chân trời sáng tạo tập trung vào việc ôn tập và củng cố các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng tính toán.
Bài tập này yêu cầu học sinh thực hiện các phép toán cơ bản với đa thức như cộng, trừ, nhân, chia đa thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép toán với đa thức và thực hiện các phép tính một cách chính xác.
Bài tập này yêu cầu học sinh thực hiện các phép toán cơ bản với phân thức đại số như cộng, trừ, nhân, chia phân thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép toán với phân thức và thực hiện các phép tính một cách chính xác.
Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về đa thức và phân thức đại số để giải quyết các bài toán phức tạp hơn. Để giải bài tập này, học sinh cần phân tích bài toán một cách kỹ lưỡng, xác định các kiến thức cần sử dụng và thực hiện các phép tính một cách chính xác.
Dưới đây là hướng dẫn giải chi tiết cho từng bài tập trong mục 2 trang 84, 85, 86 SGK Toán 8 tập 1 – Chân trời sáng tạo:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải toán:
Hy vọng rằng với hướng dẫn giải chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 84, 85, 86 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc các em học tập tốt!