Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 72 SGK Toán 8 – Chân trời sáng tạo. Bài học này thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
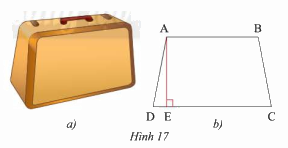
Mặt bên của một chiếc vali (Hình 17a) có dạng
Đề bài
Mặt bên của một chiếc vali (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là \(60\)cm, cạnh bên là \(61\)cm và đáy lớn là \(92\)cm. Tính độ dài đáy nhỏ.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Tính \(DE\) (sử dụng định lý Pythagore)
Tính\(AB\)
Lời giải chi tiết
Áp dụng định lý Pythagore vào tam giác vuông \(ADE\) ta có:
\(D{E^2} + A{E^2} = A{D^2}\)
\(D{E^2} = A{D^2} - A{E^2} = {61^2} - {60^2} = 121 = {11^2}\)
\(DE = 11\) (cm)
Độ dài \(AB\) là: \(92 - 11.2 = 70\) (cm)
Bài 7 trang 72 SGK Toán 8 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về các hình khối, đặc biệt là hình hộp chữ nhật và hình lập phương để tính toán diện tích bề mặt và thể tích. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là điều cần thiết để đạt kết quả tốt trong môn Toán.
Bài tập này thường bao gồm các dạng câu hỏi sau:
Để giải bài tập này một cách hiệu quả, các em cần nắm vững các công thức sau:
Ví dụ 1: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Tính diện tích bề mặt và thể tích của hình hộp chữ nhật đó.
Giải:
Diện tích bề mặt của hình hộp chữ nhật là: 2(5 x 3 + 3 x 4 + 4 x 5) = 2(15 + 12 + 20) = 2(47) = 94 cm2
Thể tích của hình hộp chữ nhật là: 5 x 3 x 4 = 60 cm3
Ví dụ 2: Một hình lập phương có cạnh 6cm. Tính diện tích bề mặt và thể tích của hình lập phương đó.
Giải:
Diện tích bề mặt của hình lập phương là: 6 x 6 x 6 = 216 cm2
Thể tích của hình lập phương là: 6 x 6 x 6 = 216 cm3
Khi giải bài tập, các em cần chú ý:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 7 trang 72 SGK Toán 8 – Chân trời sáng tạo là một bài tập quan trọng giúp các em hiểu rõ hơn về cách tính diện tích bề mặt và thể tích của các hình khối. Hy vọng với những kiến thức và phương pháp giải bài tập mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.
Giaitoan.edu.vn luôn sẵn sàng hỗ trợ các em trong mọi vấn đề liên quan đến môn Toán. Chúc các em học tập tốt!