Bài 10 trang 27 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, đầy đủ và dễ tiếp cận nhất, giúp các em học sinh tự tin hơn trong quá trình học tập môn Toán.
Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn 3 ({m^3}) nước, mỗi giờ chảy được 1 ({m^3}).
a) Tính thể tích \(y\left( {{m^3}} \right)\) của nước có trong bể sau \(x\) giờ.
Phương pháp giải:
- Giả sử mỗi giờ vòi nước chảy được \(a\) \(\left( {{m^3}} \right)\) nước vào bể thì sau \(b\) giờ lượng nước từ vào đã chảy vào được trong bể là \(a.b\)\(\left( {{m^3}} \right)\).
Lượng nước có trong bể là \(a.b + c\)\(\left( {{m^3}} \right)\) với \(c\) là lượng nước có trong bể khi chưa có vòi nước chảy vào.
Lời giải chi tiết:
Vì mỗi giờ vòi nước chảy được 1 \({m^3}\) nên sau \(x\) giờ vòi đã chảy được \(1.x\) \(\left( {{m^3}} \right)\) nước.
Ban đầu trong bể chứa sẵn 3 \({m^3}\) nước nên lượng nước \(y\) có trong bể sau \(x\) giờ là:
\(y = 1.x + 3 = x + 3\).
b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).
Phương pháp giải:
- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(A\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(B\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A\) và \(B\). Đồ thị của hàm số \(y = ax + b\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
Lời giải chi tiết:
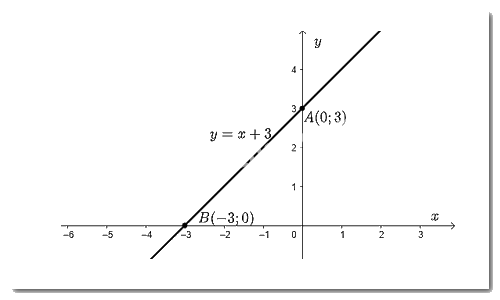
Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A;B\).
Video hướng dẫn giải
Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn 3 \({m^3}\) nước, mỗi giờ chảy được 1 \({m^3}\).
a) Tính thể tích \(y\left( {{m^3}} \right)\) của nước có trong bể sau \(x\) giờ.
Phương pháp giải:
- Giả sử mỗi giờ vòi nước chảy được \(a\) \(\left( {{m^3}} \right)\) nước vào bể thì sau \(b\) giờ lượng nước từ vào đã chảy vào được trong bể là \(a.b\)\(\left( {{m^3}} \right)\).
Lượng nước có trong bể là \(a.b + c\)\(\left( {{m^3}} \right)\) với \(c\) là lượng nước có trong bể khi chưa có vòi nước chảy vào.
Lời giải chi tiết:
Vì mỗi giờ vòi nước chảy được 1 \({m^3}\) nên sau \(x\) giờ vòi đã chảy được \(1.x\) \(\left( {{m^3}} \right)\) nước.
Ban đầu trong bể chứa sẵn 3 \({m^3}\) nước nên lượng nước \(y\) có trong bể sau \(x\) giờ là:
\(y = 1.x + 3 = x + 3\).
b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\).
Phương pháp giải:
- Để vẽ đồ thị hàm số \(y = ax + b\) ta làm như sau:
Bước 1: Cho \(x = 0 \Rightarrow y = b\) ta được điểm \(A\left( {0;b} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - b}}{a}\) ta được điểm \(B\left( {\dfrac{{ - b}}{a};0} \right)\) trên \(Ox\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A\) và \(B\). Đồ thị của hàm số \(y = ax + b\) là đường thẳng đi qua hai điểm \(A\) và \(B\).
Lời giải chi tiết:
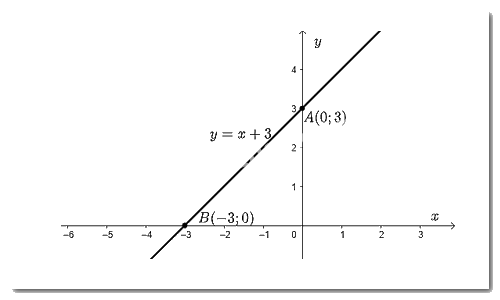
Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A;B\).
Bài 10 trang 27 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh thực hiện các phép tính đại số, cụ thể là rút gọn biểu thức và tìm giá trị của biểu thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép tính, các quy tắc về dấu ngoặc, và các công thức biến đổi đại số cơ bản.
Trước khi đi vào lời giải, chúng ta cùng xem lại đề bài một cách chi tiết:
(Đề bài đầy đủ sẽ được chèn vào đây, ví dụ: Rút gọn các biểu thức sau: a) 3x + 2y - x + 5y; b) 2(x - 3) + 5x; c) x^2 - 2x + 1)
Để giải bài tập này, chúng ta sẽ áp dụng các phương pháp sau:
Dưới đây là lời giải chi tiết cho từng phần của bài tập:
3x + 2y - x + 5y = (3x - x) + (2y + 5y) = 2x + 7y
2(x - 3) + 5x = 2x - 6 + 5x = (2x + 5x) - 6 = 7x - 6
Biểu thức x^2 - 2x + 1 có thể được viết lại dưới dạng (x - 1)^2. Do đó, x^2 - 2x + 1 = (x - 1)^2
Khi giải các bài tập về biến đổi đại số, học sinh cần chú ý những điều sau:
Để củng cố kiến thức, các em có thể thử giải các bài tập tương tự sau:
Bài 10 trang 27 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập cơ bản nhưng quan trọng trong chương trình Toán 8. Việc nắm vững các kiến thức và kỹ năng liên quan đến biến đổi đại số sẽ giúp học sinh giải quyết các bài tập phức tạp hơn trong tương lai. Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài tập và tự tin hơn trong quá trình học tập.
Chúng tôi sẽ tiếp tục cập nhật thêm nhiều lời giải và tài liệu học tập hữu ích khác. Hãy theo dõi giaitoan.edu.vn để không bỏ lỡ bất kỳ thông tin nào!