Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 SGK Chân trời sáng tạo. Mục 2 trang 65, 66 tập trung vào các kiến thức quan trọng của chương trình.
Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải đầy đủ, kèm theo các bước giải thích rõ ràng, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Đường chéo
Video hướng dẫn giải
Tìm \(x\) trong mỗi tứ giác sau:
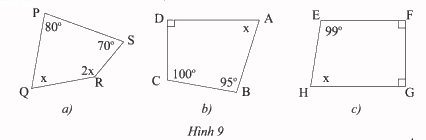
Phương pháp giải:
Sử dụng tính chất: Tổng các góc trong một tứ giác bằng \(360^\circ \)
Lời giải chi tiết:
Do tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) nên ta có:
a) Trong tứ giác \(PQRS\):
\(x + 2x = 360^\circ - \left( {80^\circ + 70^\circ } \right) = 210^\circ \)
\(3x = 210^\circ \)
\(x = 70^\circ \)
b) Trong tứ giác \(ABCD\):
\(x = 360^\circ - \left( {90^\circ + 100^\circ + 95^\circ } \right)\)
\(x = 75^\circ \)
c) Trong tứ giác \(EFGH\):
\(x = 360^\circ - \left( {99^\circ + 90^\circ + 90^\circ } \right)\)
\(x = 81^\circ \)
Video hướng dẫn giải
Đường chéo \(AC\) chia tứ giác \(ABCD\) thành hai tam giác \(ACB\) và \(ACD\) (Hình 7). Tính tổng các góc của tam giác \(ACB\) và tam giác \(ACD\). Từ đó, ta có nhận xét gì về tổng các góc của tứ giác \(ABCD\) .
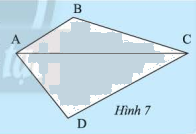
Phương pháp giải:
Sử dụng tính chất: Tổng ba góc trong một tam giác bằng \(180^\circ \)
Lời giải chi tiết:
Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)
Video hướng dẫn giải
Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.
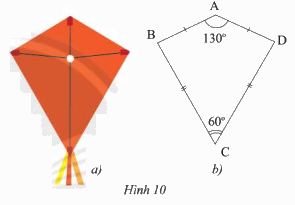
Phương pháp giải:
Sử dụng tính chất: Tổng các góc trong một tứ giác bằng \(360^\circ \)
Lời giải chi tiết:
Do tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) nên ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
\(130^\circ + \widehat B + 60^\circ + \widehat D = 360^\circ \)
\(\widehat B + \widehat D = 170^\circ \) (1)
Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = DC\) (gt)
\(AC\) chung
\( \Rightarrow \Delta ABC = \Delta ADC\) (c-c-c)
\( \Rightarrow \widehat B = \widehat D\) (hai góc tương ứng) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat D = \frac{{170^\circ }}{2} = 85^\circ \)
Video hướng dẫn giải
Đường chéo \(AC\) chia tứ giác \(ABCD\) thành hai tam giác \(ACB\) và \(ACD\) (Hình 7). Tính tổng các góc của tam giác \(ACB\) và tam giác \(ACD\). Từ đó, ta có nhận xét gì về tổng các góc của tứ giác \(ABCD\) .
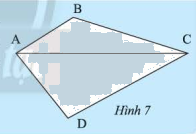
Phương pháp giải:
Sử dụng tính chất: Tổng ba góc trong một tam giác bằng \(180^\circ \)
Lời giải chi tiết:
Xét \(\Delta ABC\) ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} = 180^\circ \) (tính chất tổng ba góc trong tam giác)
Xét \(\Delta DAC\) ta có:
\(\widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ \)
Ta có:
\(\widehat B + \widehat {BAC} + \widehat {BCA} + \widehat D + \widehat {DAC} + \widehat {DCA} = 180^\circ + 180^\circ \)
\(\widehat B + \widehat D + \left( {\widehat {BAC} + \widehat {DAC}} \right) + \left( {\widehat {BCA} + \widehat {DCA}} \right) = 360^\circ \)
\(\widehat B + \widehat D + \widehat {BAD} + \widehat {BCD} = 360^\circ \)
Vậy tổng các góc của tứ giác \(ABCD\) bằng \(360^\circ \)
Video hướng dẫn giải
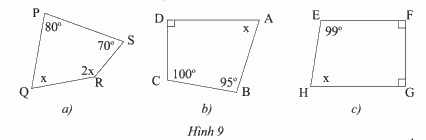
Tìm \(x\) trong mỗi tứ giác sau:
Phương pháp giải:
Sử dụng tính chất: Tổng các góc trong một tứ giác bằng \(360^\circ \)
Lời giải chi tiết:
Do tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) nên ta có:
a) Trong tứ giác \(PQRS\):
\(x + 2x = 360^\circ - \left( {80^\circ + 70^\circ } \right) = 210^\circ \)
\(3x = 210^\circ \)
\(x = 70^\circ \)
b) Trong tứ giác \(ABCD\):
\(x = 360^\circ - \left( {90^\circ + 100^\circ + 95^\circ } \right)\)
\(x = 75^\circ \)
c) Trong tứ giác \(EFGH\):
\(x = 360^\circ - \left( {99^\circ + 90^\circ + 90^\circ } \right)\)
\(x = 81^\circ \)
Video hướng dẫn giải
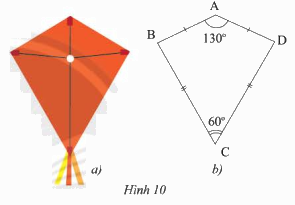
Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.
Phương pháp giải:
Sử dụng tính chất: Tổng các góc trong một tứ giác bằng \(360^\circ \)
Lời giải chi tiết:
Do tổng số đo bốn góc của một tứ giác bằng \(360^\circ \) nên ta có:
\(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
\(130^\circ + \widehat B + 60^\circ + \widehat D = 360^\circ \)
\(\widehat B + \widehat D = 170^\circ \) (1)
Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = DC\) (gt)
\(AC\) chung
\( \Rightarrow \Delta ABC = \Delta ADC\) (c-c-c)
\( \Rightarrow \widehat B = \widehat D\) (hai góc tương ứng) (2)
Từ (1) và (2) suy ra: \(\widehat B = \widehat D = \frac{{170^\circ }}{2} = 85^\circ \)
Mục 2 của chương trình Toán 8 Chân trời sáng tạo thường xoay quanh các chủ đề về hình học, cụ thể là các định lý và tính chất liên quan đến tứ giác. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Mục 2 trang 65, 66 SGK Toán 8 – Chân trời sáng tạo thường bao gồm các bài tập vận dụng các kiến thức đã học về:
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về định nghĩa và tính chất của hình thang để giải quyết. Cần xác định được các cạnh đáy, cạnh bên và các góc của hình thang để đưa ra kết luận chính xác.
Bài tập này có thể yêu cầu học sinh chứng minh một tứ giác là hình bình hành. Để làm được điều này, cần vận dụng các dấu hiệu nhận biết hình bình hành, ví dụ như chứng minh hai cặp cạnh đối song song hoặc hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Bài tập này thường liên quan đến việc tính toán các yếu tố của hình chữ nhật, ví dụ như độ dài đường chéo, diện tích, chu vi. Cần nhớ rằng hình chữ nhật có các góc vuông và các cạnh đối bằng nhau.
Bài tập này có thể yêu cầu học sinh chứng minh một tứ giác là hình thoi. Để làm được điều này, cần vận dụng các dấu hiệu nhận biết hình thoi, ví dụ như chứng minh bốn cạnh bằng nhau hoặc hai đường chéo vuông góc với nhau.
Bài toán: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Đường thẳng DE cắt đường thẳng BC tại F. Chứng minh rằng BF = FC.
Giải:
Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết các bài tập trong Mục 2 trang 65, 66 SGK Toán 8 – Chân trời sáng tạo. Chúc bạn học tập tốt!