Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 – Chân trời sáng tạo. Mục 2 trang 24 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức và kỹ năng giải bài tập.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải đáp này để giúp bạn tự tin hơn trong quá trình học tập.
Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:
Video hướng dẫn giải
Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:
a) \(4{x^2} - 9 \);
b) \({x^2}{y^2} - \dfrac{1}{4}{y^2}\)
Phương pháp giải:
Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
Lời giải chi tiết:
a) \(4{x^2} - 9 = {\left( {2x} \right)^2} - {3^2} = \left( {2x + 3} \right)\left( {2x - 3} \right)\)
b) \({x^2}{y^2} - \dfrac{1}{4}{y^2} = {\left( {xy} \right)^2} - {\left( {\dfrac{1}{2}y} \right)^2} = \left( {xy + \dfrac{1}{2}y} \right)\left( {xy - \dfrac{1}{2}y} \right)\)\( = y\left( {x + \dfrac{1}{2}} \right)y\left( {x - \dfrac{1}{2}} \right) = {y^2}\left( {x + \dfrac{1}{2}} \right)\left( {x - \dfrac{1}{2}} \right)\)
Video hướng dẫn giải
Phân tích các đa thức sau thành nhân tử:
a) \(9{x^2} - 16\) b) \(4{x^2} - 12xy + 9{y^2}\) c) \({t^3} - 8\) d) \(2a{x^3}{y^3} + 2a\)
Phương pháp giải:
a) Sử dụng hằng đăng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
b) Sử dụng hằng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)
c) Sử dụng hằng đẳng thức \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\)
d) Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\)
Lời giải chi tiết:
a) \(9{x^2} - 16\)\( = {\left( {3x} \right)^2} - {4^2} = \left( {3x + 4} \right)\left( {3x - 4} \right)\)
b) \(4{x^2} - 12xy + 9{y^2}\)\( = {\left( {2x} \right)^2} - 2.2x.3y + {\left( {3y} \right)^2} = {\left( {2x - 3y} \right)^2}\)
c) \({t^3} - 8\)\( = {t^3} - {2^3} = \left( {t - 2} \right)\left( {{t^2} + 2t + 4} \right)\)
d) \(2a{x^3}{y^3} + 2a\)\( = 2a\left( {{x^3}{y^3} + 1} \right) = 2a\left( {xy + 1} \right)\left( {{x^2}{y^2} - xy + 1} \right)\)
Video hướng dẫn giải
Tìm một hình hộp chữ nhật có thể tích \(2{x^3} - 18x\) với (\(x > 3\)) mà độ dài các cạnh đều là biểu thức chứa \(x\).
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
Ta có:
\(2{x^3} - 18x = 2x\left( {{x^2} - 9} \right) = 2x\left( {x + 3} \right)\left( {x - 3} \right)\)
Vậy hình hộp có ba kích thước là \(2x\), \(x + 3\), \(x - 3\)
Video hướng dẫn giải
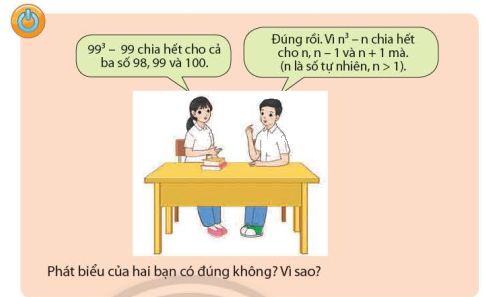
Giải đáp câu hỏi mở đầu (trang 23)
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
Ta có:
\({99^3} - 99 = 99.({99^2} - 1) = 99.\left( {99 + 1} \right).\left( {99 - 1} \right) = 99.100.98\) chia hết cho \(98\), \(99\), \(100\)
\({n^3} - n = n\left( {{n^2} - 1} \right) = n\left( {n + 1} \right)\left( {n - 1} \right)\) chia hết cho \(n\), \(n - 1\), \(n + 1\) (\(n\) là số tự nhiên, \(n > 1\))
Video hướng dẫn giải
Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:
a) \(4{x^2} - 9 \);
b) \({x^2}{y^2} - \dfrac{1}{4}{y^2}\)
Phương pháp giải:
Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
Lời giải chi tiết:
a) \(4{x^2} - 9 = {\left( {2x} \right)^2} - {3^2} = \left( {2x + 3} \right)\left( {2x - 3} \right)\)
b) \({x^2}{y^2} - \dfrac{1}{4}{y^2} = {\left( {xy} \right)^2} - {\left( {\dfrac{1}{2}y} \right)^2} = \left( {xy + \dfrac{1}{2}y} \right)\left( {xy - \dfrac{1}{2}y} \right)\)\( = y\left( {x + \dfrac{1}{2}} \right)y\left( {x - \dfrac{1}{2}} \right) = {y^2}\left( {x + \dfrac{1}{2}} \right)\left( {x - \dfrac{1}{2}} \right)\)
Video hướng dẫn giải
Phân tích các đa thức sau thành nhân tử:
a) \(9{x^2} - 16\) b) \(4{x^2} - 12xy + 9{y^2}\) c) \({t^3} - 8\) d) \(2a{x^3}{y^3} + 2a\)
Phương pháp giải:
a) Sử dụng hằng đăng thức \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)
b) Sử dụng hằng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)
c) Sử dụng hằng đẳng thức \({a^3} - {b^3} = \left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\)
d) Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức \({a^3} + {b^3} = \left( {a + b} \right)\left( {{a^2} - ab + {b^2}} \right)\)
Lời giải chi tiết:
a) \(9{x^2} - 16\)\( = {\left( {3x} \right)^2} - {4^2} = \left( {3x + 4} \right)\left( {3x - 4} \right)\)
b) \(4{x^2} - 12xy + 9{y^2}\)\( = {\left( {2x} \right)^2} - 2.2x.3y + {\left( {3y} \right)^2} = {\left( {2x - 3y} \right)^2}\)
c) \({t^3} - 8\)\( = {t^3} - {2^3} = \left( {t - 2} \right)\left( {{t^2} + 2t + 4} \right)\)
d) \(2a{x^3}{y^3} + 2a\)\( = 2a\left( {{x^3}{y^3} + 1} \right) = 2a\left( {xy + 1} \right)\left( {{x^2}{y^2} - xy + 1} \right)\)
Video hướng dẫn giải
Tìm một hình hộp chữ nhật có thể tích \(2{x^3} - 18x\) với (\(x > 3\)) mà độ dài các cạnh đều là biểu thức chứa \(x\).
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
Ta có:
\(2{x^3} - 18x = 2x\left( {{x^2} - 9} \right) = 2x\left( {x + 3} \right)\left( {x - 3} \right)\)
Vậy hình hộp có ba kích thước là \(2x\), \(x + 3\), \(x - 3\)
Video hướng dẫn giải
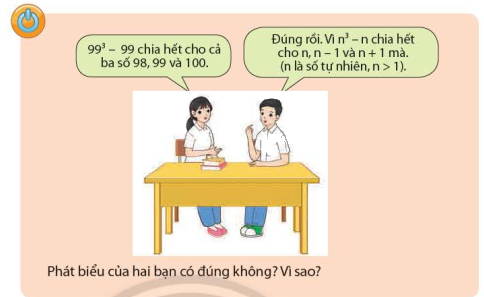
Giải đáp câu hỏi mở đầu (trang 23)
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung, hằng đẳng thức để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
Ta có:
\({99^3} - 99 = 99.({99^2} - 1) = 99.\left( {99 + 1} \right).\left( {99 - 1} \right) = 99.100.98\) chia hết cho \(98\), \(99\), \(100\)
\({n^3} - n = n\left( {{n^2} - 1} \right) = n\left( {n + 1} \right)\left( {n - 1} \right)\) chia hết cho \(n\), \(n - 1\), \(n + 1\) (\(n\) là số tự nhiên, \(n > 1\))
Mục 2 trang 24 SGK Toán 8 tập 1 – Chân trời sáng tạo thường tập trung vào các bài toán liên quan đến các phép toán với đa thức, đặc biệt là các bài toán về thu gọn đa thức, tìm bậc của đa thức và tính giá trị của đa thức tại một giá trị cụ thể của biến. Việc nắm vững các kiến thức cơ bản về đa thức là điều kiện tiên quyết để giải quyết thành công các bài toán trong mục này.
Dưới đây là giải chi tiết từng bài tập trong mục 2 trang 24 SGK Toán 8 tập 1 – Chân trời sáng tạo:
Đề bài: (Ví dụ) a) 3x2 + 2x - 5x2 + 7x - 1; b) 4xy2 - 2x2y + 3xy2 + x2y - 5.
Giải:
Đề bài: (Ví dụ) a) 5x3 - 2x2 + 1; b) -3xy2 + 4x2y - 7.
Giải:
Đề bài: (Ví dụ) a) A = x2 + 2xy - y2; b) B = 3x2 - 5xy + 2y2.
Giải:
Để giải các bài tập về đa thức một cách nhanh chóng và hiệu quả, bạn nên:
Hy vọng với bộ giải chi tiết này, bạn đã hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 24 SGK Toán 8 tập 1 – Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!