Bài 5 trang 50 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán thực tế. Bài tập này giúp củng cố lý thuyết và rèn luyện kỹ năng giải toán hình học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 50 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Tính các độ dài
Đề bài
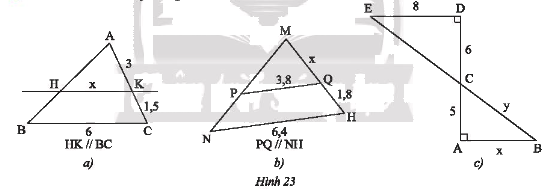
Tính các độ dài \(x,y\) trong Hình 23.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết
a) Ta có: \(AC = AK + KC = 3 + 1,5 = 4,5\)
Xét tam giác \(ABC\) có \(HK//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{HK}}{{BC}} = \frac{{AK}}{{AC}} \\ \frac{x}{6} = \frac{3}{{4,5}}\)
Do đó, \(x = \frac{{3.6}}{{4,5}} = 4\).
Vậy \(x = 4\).
b) Ta có: \(MH = MQ + QH = x + 1,8\)
Xét tam giác \(MNH\) có \(PQ//NH\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{PQ}}{{NH}} = \frac{{MQ}}{{MH}}\\ \frac{{3,8}}{{6,4}} = \frac{x}{{x + 1,8}}\)
Do đó, \(6,4x = 3,8.\left( {x + 1,8} \right)\)
\( 6,4x = 3,8x + 6,84\)
\( 6,4x - 3,8x = 6,84\)
\( 2,6x = 6,84\)
\( x = 6,84:2,6\)
\( x = \frac{{171}}{{65}}\).
Vậy \(x = \frac{{171}}{{65}}\).
c) Vì \(\left\{ \begin{array}{l}DE \bot AD\\AB \bot AD\end{array} \right.\) nên \(DE//AB\) (quan hệ từ vuông góc đến song song).
Xét \(\Delta CDE\) vuông tại \(D\) ta có:
\(E{D^2} + D{C^2} = E{C^2}\) (Định lí Py- ta – go)
\( {8^2} + {6^2} = E{C^2}\)
\( E{C^2} = 100\)
\( EC = 10\)
Xét tam giác \(ABC\) có \(DE//AB\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AC}}{{DC}} = \frac{{AB}}{{ED}} \) hay \( \frac{5}{6} = \frac{x}{8}\)
\(\frac{{AC}}{{DC}} = \frac{{BC}}{{EC}} \) hay \( \frac{5}{6} = \frac{y}{{10}}\)
Do đó, \(\left\{ \begin{array}{l}x = \frac{{5.8}}{6} = \frac{{20}}{3}\\y = \frac{{5.10}}{6} = \frac{{25}}{3}\end{array} \right.\).
Vậy \(x = \frac{{20}}{3};y = \frac{{25}}{3}\).
Bài 5 trang 50 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải hiểu rõ các khái niệm về hình hộp chữ nhật, hình lập phương, diện tích xung quanh, diện tích toàn phần và thể tích. Dưới đây là hướng dẫn giải chi tiết bài tập này:
Để tính diện tích xung quanh của hình hộp chữ nhật, ta sử dụng công thức: Diện tích xung quanh = 2 * (chiều dài + chiều rộng) * chiều cao. Trong bài toán này, ta cần xác định chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật từ thông tin đề bài cung cấp.
Ví dụ, nếu chiều dài là 5cm, chiều rộng là 3cm và chiều cao là 4cm, thì diện tích xung quanh sẽ là: 2 * (5 + 3) * 4 = 64 cm2.
Diện tích toàn phần của hình hộp chữ nhật được tính bằng công thức: Diện tích toàn phần = Diện tích xung quanh + 2 * Diện tích đáy. Diện tích đáy của hình hộp chữ nhật là chiều dài nhân với chiều rộng.
Tiếp tục ví dụ trên, diện tích đáy là 5 * 3 = 15 cm2. Vậy diện tích toàn phần sẽ là: 64 + 2 * 15 = 94 cm2.
Thể tích của hình hộp chữ nhật được tính bằng công thức: Thể tích = Chiều dài * Chiều rộng * Chiều cao. Sử dụng các giá trị chiều dài, chiều rộng và chiều cao đã cho, ta có thể dễ dàng tính được thể tích của hình hộp chữ nhật.
Trong ví dụ trên, thể tích sẽ là: 5 * 3 * 4 = 60 cm3.
Diện tích xung quanh của hình lập phương được tính bằng công thức: Diện tích xung quanh = 4 * cạnh2. Trong bài toán này, ta cần biết độ dài của một cạnh của hình lập phương.
Ví dụ, nếu cạnh của hình lập phương là 6cm, thì diện tích xung quanh sẽ là: 4 * 62 = 144 cm2.
Diện tích toàn phần của hình lập phương được tính bằng công thức: Diện tích toàn phần = 6 * cạnh2. Công thức này đơn giản hơn so với hình hộp chữ nhật vì tất cả các mặt của hình lập phương đều là hình vuông bằng nhau.
Tiếp tục ví dụ trên, diện tích toàn phần sẽ là: 6 * 62 = 216 cm2.
Thể tích của hình lập phương được tính bằng công thức: Thể tích = cạnh3. Đây là công thức đơn giản và dễ nhớ để tính thể tích của hình lập phương.
Trong ví dụ trên, thể tích sẽ là: 63 = 216 cm3.
Lưu ý:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài 5 trang 50 SGK Toán 8 tập 2 – Chân trời sáng tạo và tự tin hơn trong các bài kiểm tra Toán 8.
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong SGK Toán 8 tập 2 – Chân trời sáng tạo hoặc các bài tập trực tuyến trên giaitoan.edu.vn.
Bài 5 trang 50 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập cơ bản nhưng quan trọng trong chương trình học. Việc nắm vững các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật và hình lập phương sẽ giúp các em giải quyết các bài toán phức tạp hơn trong tương lai.