Bài 14 trang 86 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng thực tế của phương trình bậc nhất một ẩn. Bài tập này thường yêu cầu học sinh xây dựng phương trình để mô tả một tình huống thực tế và giải phương trình đó để tìm ra nghiệm.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 14 trang 86 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác
Đề bài
Cho tam giác \(ABC\)nhọn có hai đường cao \(BE,CF\) cắt nhau tại \(H\). Chứng minh rằng
a) \(\Delta AEB\backsim\Delta AFC\).
b) \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\).
c) \(\Delta HEF\backsim\Delta HCB\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Nếu tam giác vuông này có một góc nhọn bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
- Nếu \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = k\).
- Hai tam giác đồng dạng có các góc tương ứng bằng nhau.
Lời giải chi tiết
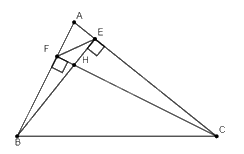
a) Vì \(BE\)là đường cao nên \(\widehat {AEB} = 90^\circ \); vì \(CF\)là đường cao nên \(\widehat {AFC} = 90^\circ \)
Xét tam giác \(AEB\) và tam giác \(AFC\) có:
\(\widehat A\) (chung)
\(\widehat {AEB} = \widehat {AFC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AEB\backsim\Delta AFC\) (g.g).
b) Vì \(\Delta AEB\backsim\Delta AFC\) nên \(\widehat {ACF} = \widehat {ABE}\) (hai góc tương ứng) hay \(\widehat {ECH} = \widehat {FBH}\).
Xét tam giác \(HEC\) và tam giác \(HFB\) có:
\(\widehat {ECH} = \widehat {FBH}\) (chứng minh trên)
\(\widehat {CEH} = \widehat {BFH} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HEC\backsim\Delta HFC\) (g.g).
Suy ra, \(\frac{{HE}}{{HF}} = \frac{{HC}}{{HB}}\) (các cặp cạnh tương ứng tỉ lệ)
Hay \(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (điều phải chứng minh).
c) Xét tam giác \(HEF\) và tam giác \(HCB\) có:
\(\widehat {FHE} = \widehat {BHC}\) (hai góc đối đỉnh)
\(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\) (chứng minh trên)
Suy ra, \(\Delta HEF\backsim\Delta HCB\) (c.g.c).
Bài 14 trang 86 SGK Toán 8 tập 2 Chân trời sáng tạo yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính toán chi phí và lợi nhuận. Cụ thể, bài toán mô tả một người nông dân trồng rau và bán rau tại chợ. Học sinh cần xác định số lượng rau cần trồng và bán để đạt được lợi nhuận mong muốn, dựa trên các thông tin về chi phí sản xuất, giá bán và số lượng rau bán được.
Để giải bài toán này, học sinh cần áp dụng các kiến thức về phương trình bậc nhất một ẩn. Các bước giải bài toán bao gồm:
Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Một người nông dân trồng rau cải trên một mảnh đất rộng 100m2. Chi phí để trồng rau là 50.000 đồng/m2. Người nông dân bán rau cải với giá 10.000 đồng/kg. Hỏi người nông dân cần trồng bao nhiêu kg rau cải để thu được lợi nhuận là 200.000 đồng?)
Lời giải:
Gọi x là số kg rau cải người nông dân cần trồng.
Chi phí trồng rau là: 100m2 * 50.000 đồng/m2 = 5.000.000 đồng
Doanh thu từ việc bán rau là: 10.000 đồng/kg * x kg = 10.000x đồng
Lợi nhuận là: Doanh thu - Chi phí = 10.000x - 5.000.000 đồng
Theo đề bài, lợi nhuận là 200.000 đồng, ta có phương trình:
10.000x - 5.000.000 = 200.000
Giải phương trình:
10.000x = 5.200.000
x = 520
Vậy người nông dân cần trồng 520 kg rau cải để thu được lợi nhuận là 200.000 đồng.
Ngoài bài 14 trang 86, SGK Toán 8 tập 2 Chân trời sáng tạo còn có nhiều bài tập tương tự về ứng dụng phương trình bậc nhất một ẩn. Các bài tập này thường yêu cầu học sinh giải quyết các bài toán thực tế liên quan đến các lĩnh vực khác nhau như kinh doanh, du lịch, xây dựng,...
Để học tốt Toán 8, học sinh có thể tham khảo thêm các tài liệu sau:
Bài 14 trang 86 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc nhất một ẩn và ứng dụng kiến thức vào thực tế. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải bài tập này và các bài tập tương tự.