Bài 10 trang 72 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 72 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Đường đi và khoảng cách từ nhà anh Thanh
Đề bài
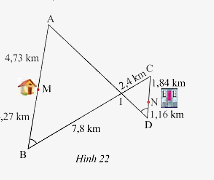
Đường đi và khoảng cách từ nhà anh Thanh (điểm \(M\)) đến công ty (điểm \(N\)) được thể hiện trong Hình 22. Hãy tìm con đường ngắn nhất để đi từ nhà anh Thanh đến công ty.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau.
- Hai tam giác đồng dạng thì các cặp cạnh tương ứng có cùng tỉ lệ.
Lời giải chi tiết
Ta có: \(AB = AM + MB = 4,73 + 4,27 = 9m\);\(CD = CN + ND = 1,84 + 1,16 = 3m\)
Xét tam giác \(AIB\) tam giác \(CID\) ta có:
\(\widehat {ABI} = \widehat {CDI}\) (giả thiết)
\(\widehat {AIB} = \widehat {CID}\) (hai góc đối đỉnh)
Do đó, \(\Delta AIB\backsim\Delta CID\) (g.g)
Suy ra, \(\frac{{AB}}{{CD}} = \frac{{AI}}{{CI}} = \frac{{BI}}{{DI}}\)
\(\frac{9}{3} = \frac{{AI}}{{2,4}} = \frac{{7,8}}{{DI}}\).
Ta có:
\(\frac{9}{3} = \frac{{AI}}{{2,4}} \) suy ra \(AI = \frac{{9.2,4}}{3} = 7,2m\);
\(\frac{9}{3} = \frac{{7,8}}{{ID}} \) suy ra \(ID = \frac{{3.7,8}}{9} = 2,6m\).
Các con đường đi từ nhà anh Thanh đến công ty là:
Con đường: \(MB \to BI \to IC \to CN\) có độ dài là:
\(MB + BI + IC + CN = 4,27 + 7,8 + 2,4 + 1,84 = 16,31km\)
Con đường: \(MB \to BI \to ID \to DN\) có độ dài là:
\(MB + BI + ID + DN = 4,27 + 7,8 + 2,6 + 1,16 = 15,83km\)
Con đường: \(MA \to AI \to ID \to DN\) có độ dài là:
\(MA + AI + ID + DN = 4,73 + 7,2 + 2,6 + 1,16 = 15,69km\)
Con đường: \(MA \to AI \to IC \to CN\) có độ dài là:
\(MA + AI + IC + CN = 4,73 + 7,2 + 2,4 + 1,84 = 16,17km\)
Vậy đi theo con đường \(MA \to AI \to ID \to DN\) là ngắn nhất.
Bài 10 trang 72 SGK Toán 8 tập 2 – Chân trời sáng tạo thường xoay quanh việc áp dụng các quy tắc về phép nhân đa thức, phép chia đa thức và các hằng đẳng thức đáng nhớ. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 10. Tuy nhiên, dựa trên cấu trúc chung của SGK Toán 8 tập 2 – Chân trời sáng tạo, bài tập này thường có dạng như sau:
Ví dụ: Phân tích đa thức thành nhân tử: x^2 - 4x + 4
Lời giải:
x^2 - 4x + 4 = x^2 - 2.x.2 + 2^2 = (x - 2)^2
Trong ví dụ trên, chúng ta đã sử dụng hằng đẳng thức (a-b)^2 = a^2 - 2ab + b^2 để phân tích đa thức thành nhân tử.
Ngoài dạng bài tập phân tích đa thức thành nhân tử, bài 10 trang 72 SGK Toán 8 tập 2 – Chân trời sáng tạo còn có thể xuất hiện các dạng bài tập sau:
Để giải quyết các dạng bài tập này, học sinh cần:
Để học tốt môn Toán 8, đặc biệt là các bài tập về đa thức, học sinh nên:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài 10 trang 72 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bằng cách nắm vững kiến thức cơ bản, luyện tập thường xuyên và áp dụng các phương pháp giải phù hợp, các em học sinh có thể tự tin giải quyết bài tập này một cách hiệu quả.