Bài 5 trang 72 SGK Toán 8 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các tình huống khác.
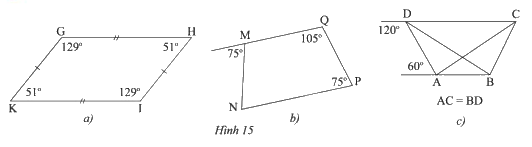
Tứ giác nào trong Hình 15 là hình thang cân?
Đề bài
Tứ giác nào trong Hình 15 là hình thang cân?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng dấu hiệu nhận biết hình thang cân
Lời giải chi tiết
a) Xét tứ giác \(KGHI\) ta có:
\(\widehat {{\rm{HGK}}} + \widehat {{\rm{GKI}}} = 129^\circ + 51^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(GH\;{\rm{//}}\;KI\)
Suy ra \(KGHI\) là hình thang
b)
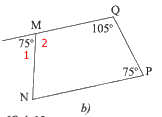
Ta có:
\(\widehat {M_1} + \widehat {M_2} = 180^0\) (hai góc kề bù)
\(\Rightarrow \widehat{M_2} = 180^0 - \widehat{M_1} = 180^0 - 75^0 = 105^0\)
Xét tứ giác MNPQ có: \(\widehat {M_2} + \widehat N + \widehat P + \widehat Q = 360^0 \Rightarrow \widehat N = 360^0 - \widehat {M_2} - \widehat P - \widehat Q = 360^0 - 105^0 - 75^0 - 105^0 = 75^0\)
Ta có: \(\widehat {M_1} = \widehat N = 75^0\) mà \(\widehat {M_1}\) và \( \widehat N\) ở vị trí so le trong nên MQ //NP suy ra MNPQ là hình thang.
Mà \(\widehat {M_2} = \widehat Q = 105^0; \widehat {N} = \widehat P = 75^0\)
Suy ra \(MNPQ\) là hình thang cân
c)
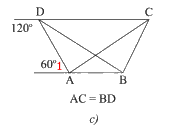
Ta có:
\(\widehat {{\rm{ADC}}} = 180^\circ - 120^\circ = 60^\circ \)
Ta có: \(\widehat {{\rm{ADC}}} = \widehat {{A_1}} = 60^\circ \)
Mà hai góc ở vị trí so le trong
Suy ra \(AB\) // \(CD\)
Suy ra \(ABCD\) là hình thang
Mà \(AC = BD\)
Suy ra \(ABCD\) là hình thang cân
Bài 5 trang 72 SGK Toán 8 – Chân trời sáng tạo yêu cầu học sinh thực hiện các phép biến đổi đại số để rút gọn biểu thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về dấu ngoặc, quy tắc chuyển vế, và các phép toán cơ bản.
Bài tập yêu cầu rút gọn các biểu thức sau:
a) (x + 3)(x - 3)
Áp dụng hằng đẳng thức (a + b)(a - b) = a^2 - b^2, ta có:
(x + 3)(x - 3) = x^2 - 3^2 = x^2 - 9
b) (2x - 1)^2
Áp dụng hằng đẳng thức (a - b)^2 = a^2 - 2ab + b^2, ta có:
(2x - 1)^2 = (2x)^2 - 2(2x)(1) + 1^2 = 4x^2 - 4x + 1
c) (x + 1)(x^2 - x + 1)
Áp dụng hằng đẳng thức (a + b)(a^2 - ab + b^2) = a^3 + b^3, ta có:
(x + 1)(x^2 - x + 1) = x^3 + 1^3 = x^3 + 1
d) (x - 2)(x^2 + 2x + 4)
Áp dụng hằng đẳng thức (a - b)(a^2 + ab + b^2) = a^3 - b^3, ta có:
(x - 2)(x^2 + 2x + 4) = x^3 - 2^3 = x^3 - 8
Khi thực hiện các phép biến đổi đại số, học sinh cần chú ý đến dấu của các số hạng và áp dụng đúng các quy tắc. Việc sử dụng hằng đẳng thức một cách linh hoạt sẽ giúp rút gọn biểu thức nhanh chóng và chính xác.
Ngoài các hằng đẳng thức đã sử dụng, học sinh cũng cần nắm vững các hằng đẳng thức khác như (a + b)^2 = a^2 + 2ab + b^2, (a - b)^2 = a^2 - 2ab + b^2, (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3, (a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3. Việc hiểu rõ và áp dụng các hằng đẳng thức này sẽ giúp học sinh giải quyết nhiều bài tập đại số phức tạp hơn.
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự sau:
Bài 5 trang 72 SGK Toán 8 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Bằng cách nắm vững các quy tắc và hằng đẳng thức, học sinh có thể giải bài tập này một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải cụ thể, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.
Việc luyện tập thường xuyên và áp dụng kiến thức vào thực tế sẽ giúp các em hiểu sâu hơn về môn Toán và đạt kết quả tốt trong học tập.