Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 79, 80 SGK Toán 8 tập 2 – Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập trong mục này tập trung vào các kiến thức quan trọng của chương trình Toán 8, đòi hỏi các em phải vận dụng linh hoạt các định lý, công thức đã học.
Cho hai hình đồng dạng phối cảnh
Video hướng dẫn giải
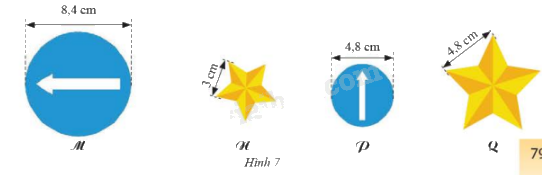
Trong hình 7 dưới đây, hãy chọn ra các cặp hình đồng dạng với nhau. Tìm tỉ số đồng dạng tương ứng.
Phương pháp giải:
Hai hình \(H\) và hình \(H'\) được gọi là đồng dạng nếu có hình đồng dạng phối của của hình \(H\) bằng hình \(H'\).
Lời giải chi tiết:
Hình M và P đồng dạng theo tỉ số \( k = \frac {8,4}{4,8} = \frac {7}{4} \)
Hình N và Q đồng dạng theo tỉ số \( k = \frac {3}{4,8} = \frac {5}{8} \)
Video hướng dẫn giải
Trong hình 5, biết \(H_1\) đồng dạng phối cảnh với hình H tỉ số \(k = \frac{3}{2}\).
a) Tính \(x,y\).
b) So sánh hình \({H_1}\) và hình \(H'\).

Phương pháp giải:
- Ta tính \(x,y\) dựa vào tỉ số đồng dạng của hai hình.
Lời giải chi tiết:
a) Vì hai hình đồng dạng phối cảnh \(H\) và \({H_1}\) có tỉ số đồng dạng \(k = \frac{2}{3}\) nên \(\frac{{3,6}}{x} = \frac{2}{y} = \frac{2}{3} \Rightarrow \left\{ \begin{array}{l}\frac{{3,6}}{x} = \frac{2}{3}\\\frac{2}{y} = \frac{2}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 5,4\\y = 3\end{array} \right.\)
Vậy \(x = 5,4cm;y = 3cm\).
b) Hình \({H_1}\) và hình \(H'\) là hai hình bằng nhau vì chúng có kích thước bằng nhau và khi ta đặt hình \({H_1}\) nằm ngang sẽ thu được hình \(H'\).
Video hướng dẫn giải
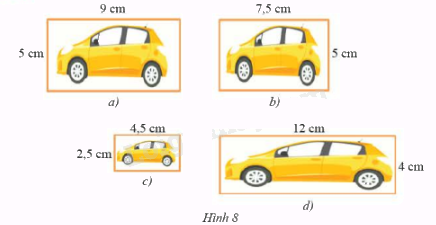
Trong Hình 8b, c, d, Hình nào đồng dạng với Hình 8a. Giải thích.
Phương pháp giải:
Hai hình \(H\) và hình \(H'\) được gọi là đồng dạng nếu có hình đồng dạng phối của của hình \(H\) bằng hình \(H'\).
Lời giải chi tiết:
- Xét hình 8a và hình 8b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8b lần lượt là:
\(\frac{9}{{7,5}} = 1,2;\frac{5}{5} = 1\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 8b. Do đó, hình 8a và hình 8b không đồng dạng với nhau.
- Xét hình 8a và hình 8c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8c lần lượt là:
\(\frac{9}{{4,5}} = 2;\frac{5}{{2,5}} = 2\). Do đó, tồn tại hình động dạng phối cảnh của hình 8a bằng hình 8c (hình 8a thu nhỏ với tỉ số 2). Do đó, hình 8a và hình 8c đồng dạng với nhau.
- Xét hình 8a và hình 8d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8d lần lượt là:
\(\frac{9}{{12}} = 0,75;\frac{5}{4} = 1,25\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 8b. Do đó, hình 8a và hình 8b không đồng dạng với nhau.
Video hướng dẫn giải
Trong hình 5, biết \(H_1\) đồng dạng phối cảnh với hình H tỉ số \(k = \frac{3}{2}\).
a) Tính \(x,y\).
b) So sánh hình \({H_1}\) và hình \(H'\).

Phương pháp giải:
- Ta tính \(x,y\) dựa vào tỉ số đồng dạng của hai hình.
Lời giải chi tiết:
a) Vì hai hình đồng dạng phối cảnh \(H\) và \({H_1}\) có tỉ số đồng dạng \(k = \frac{2}{3}\) nên \(\frac{{3,6}}{x} = \frac{2}{y} = \frac{2}{3} \Rightarrow \left\{ \begin{array}{l}\frac{{3,6}}{x} = \frac{2}{3}\\\frac{2}{y} = \frac{2}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 5,4\\y = 3\end{array} \right.\)
Vậy \(x = 5,4cm;y = 3cm\).
b) Hình \({H_1}\) và hình \(H'\) là hai hình bằng nhau vì chúng có kích thước bằng nhau và khi ta đặt hình \({H_1}\) nằm ngang sẽ thu được hình \(H'\).
Video hướng dẫn giải
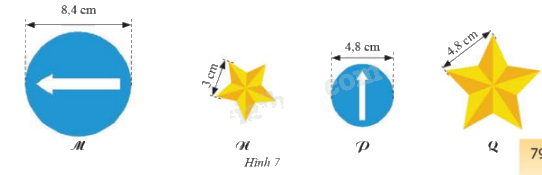
Trong hình 7 dưới đây, hãy chọn ra các cặp hình đồng dạng với nhau. Tìm tỉ số đồng dạng tương ứng.
Phương pháp giải:
Hai hình \(H\) và hình \(H'\) được gọi là đồng dạng nếu có hình đồng dạng phối của của hình \(H\) bằng hình \(H'\).
Lời giải chi tiết:
Hình M và P đồng dạng theo tỉ số \( k = \frac {8,4}{4,8} = \frac {7}{4} \)
Hình N và Q đồng dạng theo tỉ số \( k = \frac {3}{4,8} = \frac {5}{8} \)
Video hướng dẫn giải
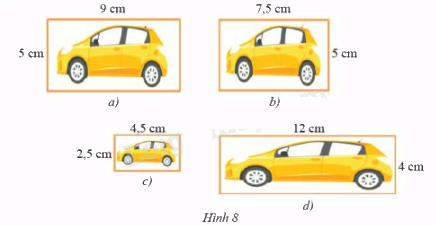
Trong Hình 8b, c, d, Hình nào đồng dạng với Hình 8a. Giải thích.
Phương pháp giải:
Hai hình \(H\) và hình \(H'\) được gọi là đồng dạng nếu có hình đồng dạng phối của của hình \(H\) bằng hình \(H'\).
Lời giải chi tiết:
- Xét hình 8a và hình 8b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8b lần lượt là:
\(\frac{9}{{7,5}} = 1,2;\frac{5}{5} = 1\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 8b. Do đó, hình 8a và hình 8b không đồng dạng với nhau.
- Xét hình 8a và hình 8c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8c lần lượt là:
\(\frac{9}{{4,5}} = 2;\frac{5}{{2,5}} = 2\). Do đó, tồn tại hình động dạng phối cảnh của hình 8a bằng hình 8c (hình 8a thu nhỏ với tỉ số 2). Do đó, hình 8a và hình 8c đồng dạng với nhau.
- Xét hình 8a và hình 8d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8d lần lượt là:
\(\frac{9}{{12}} = 0,75;\frac{5}{4} = 1,25\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 8b. Do đó, hình 8a và hình 8b không đồng dạng với nhau.
Mục 2 trang 79, 80 SGK Toán 8 tập 2 – Chân trời sáng tạo là một phần quan trọng trong chương trình học, tập trung vào việc củng cố và mở rộng kiến thức về các hình khối trong không gian. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, các định lý liên quan và các phương pháp chứng minh hình học.
Mục 2 thường bao gồm các bài tập về:
Để giải các bài tập trong Mục 2, học sinh có thể áp dụng các phương pháp sau:
Đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA vuông góc với mặt phẳng (ABCD). Tính thể tích của hình chóp S.ABCD.
Lời giải:
Diện tích đáy ABCD là: Sđáy = a2
Chiều cao của hình chóp là: h = SA
Thể tích của hình chóp S.ABCD là: V = (1/3) * Sđáy * h = (1/3) * a2 * SA
Đề bài: Cho hình lăng trụ đứng ABC.DEF có đáy ABC là tam giác vuông tại A, AB = 3cm, AC = 4cm, AD = 5cm. Tính diện tích xung quanh của hình lăng trụ.
Lời giải:
Chu vi đáy ABC là: P = AB + AC + BC = 3 + 4 + 5 = 12cm
Diện tích xung quanh của hình lăng trụ là: Sxq = P * AD = 12 * 5 = 60cm2
Khi giải các bài tập về hình học không gian, học sinh cần chú ý:
Việc nắm vững kiến thức và phương pháp giải bài tập trong Mục 2 trang 79, 80 SGK Toán 8 tập 2 – Chân trời sáng tạo là rất quan trọng để học sinh có thể tự tin giải các bài tập toán học và đạt kết quả tốt trong các kỳ thi. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ hiểu rõ hơn về nội dung bài học và có thể áp dụng vào thực tế một cách hiệu quả.
| Hình khối | Công thức tính diện tích xung quanh | Công thức tính thể tích |
|---|---|---|
| Hình chóp | Sxq = (1/2) * P * l (P là chu vi đáy, l là trung đoạn) | V = (1/3) * Sđáy * h (h là chiều cao) |
| Hình lăng trụ đứng | Sxq = P * h (P là chu vi đáy, h là chiều cao) | V = Sđáy * h (h là chiều cao) |