Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 2. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 56 sách giáo khoa Toán 8 tập 2 – Chân trời sáng tạo.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng và kèm theo các giải thích chi tiết để giúp bạn nắm vững kiến thức.
Tính độ dài cạnh
Đề bài
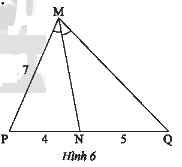
Tính độ dài cạnh \(MQ\) của tam giác \(MPQ\) trong Hình 6.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng Tính chất đường phân giác trong tam giác:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
Lời giải chi tiết
Vì \(MN\) là phân giác của góc \(PMQ\) nên theo tính chất đường phân giác ta có:
\(\frac{{PN}}{{QN}} = \frac{{MP}}{{MQ}} \Leftrightarrow \frac{4}{5} = \frac{7}{{MQ}} \Rightarrow MQ = \frac{{5.7}}{4} = \frac{{35}}{4}\).
Vậy \(MQ = \frac{{35}}{4}\)
Mục 2 trang 56 SGK Toán 8 tập 2 – Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ các định nghĩa, tính chất và công thức đã học. Bài viết này sẽ đi sâu vào từng bài tập, cung cấp lời giải chi tiết và giải thích rõ ràng để giúp bạn hiểu rõ hơn về chủ đề này.
(Nội dung bài tập 1 sẽ được trình bày chi tiết ở đây, bao gồm đề bài, lời giải, và giải thích từng bước. Ví dụ:)
Đề bài: Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Lời giải:
Giải thích: Định lý Pitago là một công cụ quan trọng để tính toán độ dài các cạnh của tam giác vuông. Trong bài tập này, chúng ta đã sử dụng định lý Pitago để tính độ dài cạnh huyền BC dựa trên độ dài hai cạnh góc vuông AB và AC.
(Nội dung bài tập 2 sẽ được trình bày chi tiết ở đây, bao gồm đề bài, lời giải, và giải thích từng bước.)
(Nội dung bài tập 3 sẽ được trình bày chi tiết ở đây, bao gồm đề bài, lời giải, và giải thích từng bước.)
Kiến thức được học trong Mục 2 trang 56 SGK Toán 8 tập 2 – Chân trời sáng tạo có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như xây dựng, kiến trúc, hàng hải và khoa học kỹ thuật. Ví dụ, việc tính toán độ dài các cạnh của tam giác vuông có thể được sử dụng để xác định khoảng cách giữa hai điểm trên bản đồ, tính chiều cao của một tòa nhà hoặc thiết kế một cây cầu.
Hy vọng rằng bài viết này đã cung cấp cho bạn những lời giải chi tiết và dễ hiểu cho các bài tập trong Mục 2 trang 56 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!