Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 68, 69 sách giáo khoa Toán 8 Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Tứ giác
Video hướng dẫn giải
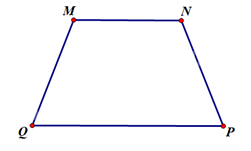
Tìm các góc chưa biết của hình thang \(MNPQ\) có hai đáy là \(MN\) và \(QP\) trong mỗi trường hợp sau.
a) \(\widehat Q = 90^\circ \) và \(\widehat N = 125^\circ \)
b) \(\widehat P = \widehat Q = 110^\circ \)
Phương pháp giải:
Sử dụng kiến thức về hình thang, hình thang cân, hình thang vuông
Lời giải chi tiết:
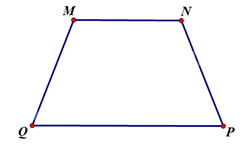
a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)
Video hướng dẫn giải
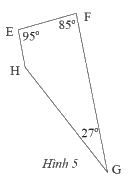
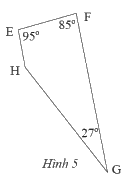
Tứ giác \(EFGH\) có các góc cho như trong Hình 5.
a) Chứng minh rằng \(EFGH\) là hình thang
b) Tìm góc chưa biết của tứ giác
Phương pháp giải:
a) Chứng minh \(EH\) // \(FG\)
b) Sử dụng định lý tổng bốn góc của tứ giác bằng \(360^0\)
Lời giải chi tiết:
a) Ta có:
\(\widehat {\rm{E}} + \widehat {\rm{F}} = 95^\circ + 85^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(EH\;{\rm{//}}\;FG\)
Suy ra \(EFGH\) là hình thang
b) Xét hình thang \(EFGH\) ta có: \(\widehat E + \widehat F + \widehat G + \widehat H = 360^\circ \)
\(\begin{array}{l}95^\circ + 85^\circ + 27^\circ + \widehat H = 360^\circ \\\widehat H = 153^\circ \end{array}\)
Video hướng dẫn giải
Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân \(ABCD\) (hình 4). Cho biết \(\widehat D = \widehat C = 75^\circ \). Tìm số đo \(\widehat A\) và \(\widehat B\).

Phương pháp giải:
Sử dụng định nghĩa hình thang cân.
Lời giải chi tiết:
Do ${ABCD}$ là hình thang cân (gt) nên \(\widehat A = \widehat B\)
Xét hình thang \(ABCD\) ta có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} + \widehat {\rm{D}} = 360^\circ \)
\(\begin{array}{l}\widehat A + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat A + \widehat B = 210^\circ \end{array}\)
Mà \(\widehat A = \widehat B\) (cmt)
Suy ra : \(\widehat {\rm{A}} = \widehat B = 105^\circ \)
Video hướng dẫn giải
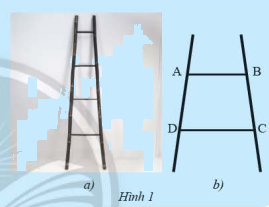
Tứ giác \(ABCD\) (Hình 1b) là hình vẽ minh họa một phần của chiếc thang ở Hình 1a. Nêu nhận xét của em về hai cạnh \(AB\) và \(CD\) của tứ giác này.
Phương pháp giải:
Quan sát, sử dụng kiến thức về hai đường thẳng song song
Lời giải chi tiết:
Hai cạnh \(AB\) và \(CD\) song song với nhau
Video hướng dẫn giải
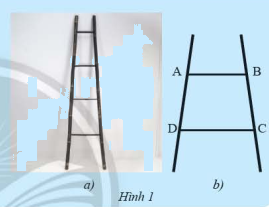
Tứ giác \(ABCD\) (Hình 1b) là hình vẽ minh họa một phần của chiếc thang ở Hình 1a. Nêu nhận xét của em về hai cạnh \(AB\) và \(CD\) của tứ giác này.
Phương pháp giải:
Quan sát, sử dụng kiến thức về hai đường thẳng song song
Lời giải chi tiết:
Hai cạnh \(AB\) và \(CD\) song song với nhau
Video hướng dẫn giải
Tìm các góc chưa biết của hình thang \(MNPQ\) có hai đáy là \(MN\) và \(QP\) trong mỗi trường hợp sau.
a) \(\widehat Q = 90^\circ \) và \(\widehat N = 125^\circ \)
b) \(\widehat P = \widehat Q = 110^\circ \)
Phương pháp giải:
Sử dụng kiến thức về hình thang, hình thang cân, hình thang vuông
Lời giải chi tiết:
a) Hình thang \(MNPQ\) có \(\widehat Q = 90^\circ \) nên là hình thang vuông. Suy ra \(\widehat M = 90^\circ \)
Áp dụng định lí tổng các góc của một tứ giác, ta có: \(\widehat P = 360^\circ - \left( {90^\circ + 90^\circ + 125^\circ } \right) = 55^\circ \)
b) Hình thang \(MNPQ\) có \(\widehat P = \widehat Q = 110^\circ \) nên là hình thang cân.
Suy ra \(\widehat M = \widehat N = 180^\circ - 110^\circ = 70^\circ \)
Video hướng dẫn giải
Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân \(ABCD\) (hình 4). Cho biết \(\widehat D = \widehat C = 75^\circ \). Tìm số đo \(\widehat A\) và \(\widehat B\).

Phương pháp giải:
Sử dụng định nghĩa hình thang cân.
Lời giải chi tiết:
Do ${ABCD}$ là hình thang cân (gt) nên \(\widehat A = \widehat B\)
Xét hình thang \(ABCD\) ta có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} + \widehat {\rm{D}} = 360^\circ \)
\(\begin{array}{l}\widehat A + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat A + \widehat B = 210^\circ \end{array}\)
Mà \(\widehat A = \widehat B\) (cmt)
Suy ra : \(\widehat {\rm{A}} = \widehat B = 105^\circ \)
Video hướng dẫn giải
Tứ giác \(EFGH\) có các góc cho như trong Hình 5.
a) Chứng minh rằng \(EFGH\) là hình thang
b) Tìm góc chưa biết của tứ giác
Phương pháp giải:
a) Chứng minh \(EH\) // \(FG\)
b) Sử dụng định lý tổng bốn góc của tứ giác bằng \(360^0\)
Lời giải chi tiết:
a) Ta có:
\(\widehat {\rm{E}} + \widehat {\rm{F}} = 95^\circ + 85^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(EH\;{\rm{//}}\;FG\)
Suy ra \(EFGH\) là hình thang
b) Xét hình thang \(EFGH\) ta có: \(\widehat E + \widehat F + \widehat G + \widehat H = 360^\circ \)
\(\begin{array}{l}95^\circ + 85^\circ + 27^\circ + \widehat H = 360^\circ \\\widehat H = 153^\circ \end{array}\)
Mục 1 trang 68, 69 SGK Toán 8 Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng thu gọn đa thức, tìm bậc của đa thức, và thực hiện các phép cộng, trừ đa thức. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các kiến thức nâng cao hơn trong chương trình Toán 8.
Bài 1 yêu cầu học sinh thu gọn các đa thức đã cho. Để thu gọn đa thức, ta cần thực hiện các phép cộng, trừ các đơn thức đồng dạng. Ví dụ, để thu gọn đa thức 3x2 + 2x - x2 + 5x, ta thực hiện như sau:
Bài 2 yêu cầu học sinh tìm bậc của các đa thức đã cho. Bậc của đa thức là bậc của đơn thức có bậc cao nhất trong đa thức đó. Ví dụ, để tìm bậc của đa thức 5x3 - 2x2 + x - 1, ta thực hiện như sau:
Bài 3 yêu cầu học sinh thực hiện phép cộng hoặc trừ các đa thức đã cho. Để cộng hoặc trừ các đa thức, ta cần thực hiện các phép cộng, trừ các đơn thức đồng dạng. Ví dụ, để cộng hai đa thức A = 2x2 + 3x - 1 và B = -x2 + x + 2, ta thực hiện như sau:
Để giải nhanh các bài tập về đa thức, các em cần nắm vững các quy tắc sau:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, các em học sinh đã nắm vững kiến thức và kỹ năng giải các bài tập trong mục 1 trang 68, 69 SGK Toán 8 Chân trời sáng tạo. Chúc các em học tập tốt!