Bài 13 trang 29 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các phép biến đổi đại số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, đầy đủ và dễ tiếp cận nhất, giúp các em học sinh tự tin hơn trong quá trình học tập môn Toán.
Cho biết đồ thị của hàm số (y = ax) đi qua điểm
a) Xác định hệ số \(a\).
Phương pháp giải:
- Hàm số \(y = ax\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0}\)
Lời giải chi tiết:
a) Vì đồ thị hàm số đi\(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\) nên ta có:
\(\dfrac{{ - 4}}{5} = a.1 \Rightarrow a = \dfrac{{ - 4}}{5}\).
Vậy hệ số góc của đường thẳng là \(a = \dfrac{{ - 4}}{5}\).
Video hướng dẫn giải
Cho biết đồ thị của hàm số \(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\).
a) Xác định hệ số \(a\).
Phương pháp giải:
- Hàm số \(y = ax\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0}\)
Lời giải chi tiết:
a) Vì đồ thị hàm số đi\(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\) nên ta có:
\(\dfrac{{ - 4}}{5} = a.1 \Rightarrow a = \dfrac{{ - 4}}{5}\).
Vậy hệ số góc của đường thẳng là \(a = \dfrac{{ - 4}}{5}\).
b) Vẽ điểm trên đồ thị có hoành độ bằng \( - 5\).
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = \dfrac{{ - 4}}{5}x\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(O\) và \(P\).
Từ điểm \(x = - 5\) trên \(Ox\)vẽ đường thẳng vuông góc với \(Ox\) cắt đồ thị hàm số tại điểm \(B\). Khi đó, điểm \(B\) là điểm trên đồ thị hàm số có hoành độ bằng -5.
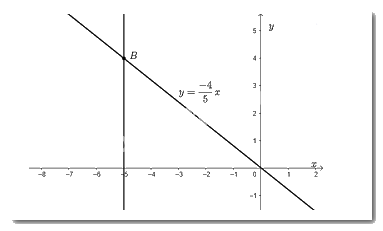
c) Vẽ điểm trên đồ thị có tung độ bằng 2.
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết:
Từ điểm \(y = 2\) trên \(Oy\)vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.
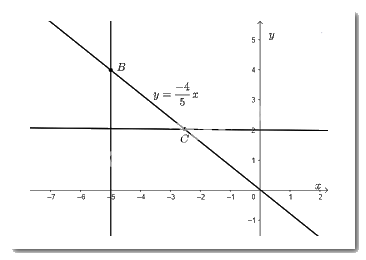
c) Vẽ điểm trên đồ thị có tung độ bằng 2.
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết:
Từ điểm \(y = 2\) trên \(Oy\)vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.
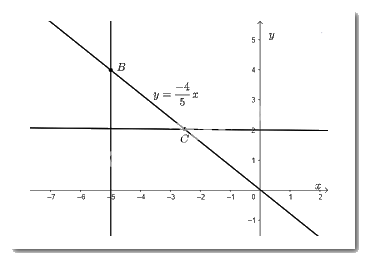
b) Vẽ điểm trên đồ thị có hoành độ bằng \( - 5\).
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax\), ta thường thực hiện các bước sau:
Bước 1: Xác định một điểm \(M\) trên đồ thị khác gốc tọa độ \(O\), chẳng hạn \(M\left( {1;a} \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(O\) và \(M\).
Lời giải chi tiết:
Vẽ đồ thị hàm số \(y = \dfrac{{ - 4}}{5}x\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(O\) và \(P\).
Từ điểm \(x = - 5\) trên \(Ox\)vẽ đường thẳng vuông góc với \(Ox\) cắt đồ thị hàm số tại điểm \(B\). Khi đó, điểm \(B\) là điểm trên đồ thị hàm số có hoành độ bằng -5.
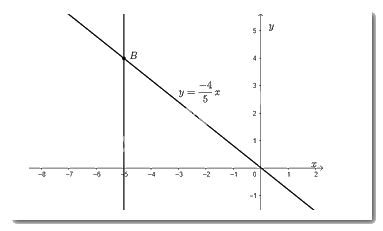
Bài 13 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo yêu cầu học sinh thực hiện các phép tính đại số, cụ thể là rút gọn biểu thức và tìm giá trị của biểu thức. Để giải bài tập này, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép tính, các quy tắc về dấu ngoặc, và các quy tắc về phép cộng, trừ, nhân, chia đa thức.
Bài 13 yêu cầu học sinh thực hiện các phép tính sau:
1. Rút gọn biểu thức (3x + 2)(x - 1):
Để rút gọn biểu thức này, ta sử dụng công thức phân phối (a + b)(c + d) = ac + ad + bc + bd:
(3x + 2)(x - 1) = 3x * x + 3x * (-1) + 2 * x + 2 * (-1) = 3x2 - 3x + 2x - 2 = 3x2 - x - 2
2. Tìm giá trị của biểu thức 2x2 - 5x + 3 khi x = 2:
Để tìm giá trị của biểu thức, ta thay x = 2 vào biểu thức:
2 * (2)2 - 5 * (2) + 3 = 2 * 4 - 10 + 3 = 8 - 10 + 3 = 1
3. Giải phương trình 4x - 8 = 0:
Để giải phương trình này, ta chuyển -8 sang vế phải:
4x = 8
Sau đó, ta chia cả hai vế cho 4:
x = 8 / 4 = 2
Các bài tập về phép tính đại số là nền tảng quan trọng để học sinh tiếp thu các kiến thức nâng cao hơn trong môn Toán, như giải phương trình bậc hai, giải hệ phương trình, và các bài toán về hàm số. Việc rèn luyện kỹ năng về phép tính đại số một cách thường xuyên sẽ giúp học sinh tự tin hơn trong quá trình học tập môn Toán.
Ngoài ra, học sinh có thể tham khảo thêm các tài liệu học tập khác, như sách bài tập, đề thi thử, và các trang web học toán online để nâng cao kiến thức và kỹ năng của mình.
Hãy xét biểu thức: (x + 3)(x - 2) + 5
Rút gọn biểu thức này:
(x + 3)(x - 2) + 5 = x2 - 2x + 3x - 6 + 5 = x2 + x - 1
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải Bài 13 trang 29 SGK Toán 8 tập 2 – Chân trời sáng tạo. Chúc các em học tập tốt!
| Phép tính | Kết quả |
|---|---|
| (3x + 2)(x - 1) | 3x2 - x - 2 |
| 2x2 - 5x + 3 (khi x=2) | 1 |
| 4x - 8 = 0 | x = 2 |