Chào mừng bạn đến với bài học lý thuyết Hằng đẳng thức đáng nhớ trong chương trình Toán 8 - Chân trời sáng tạo tại giaitoan.edu.vn. Đây là một trong những kiến thức nền tảng quan trọng giúp bạn giải quyết các bài toán đại số một cách hiệu quả.
Bài viết này sẽ cung cấp đầy đủ các hằng đẳng thức đáng nhớ, phương pháp chứng minh và ứng dụng của chúng trong việc giải toán. Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất với nội dung được trình bày rõ ràng, dễ hiểu.
Bình phương của một tổng là gì?
1. Bình phương của một tổng
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Ví dụ: \({101^2} = {(100 + 1)^2} = {100^2} + 2.100.1 + {1^2} = 10201\)
2. Bình phương của một hiệu
\({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Ví dụ: \({99^2} = {(100 - 1)^2} = {100^2} - 2.100.1 + {1^2} = 9801\)
3. Hiệu hai bình phương
\({A^2} - {B^2} = (A - B)(A + B)\)
Ví dụ: \({101^2} - {99^2} = (101 - 99)(101 + 99) = 2.200 = 400\)
4. Lập phương của một tổng
\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)
Ví dụ: \({\left( {x + 3} \right)^3} = {x^3} + 3{x^2}.3 + 3x{.3^2} + {3^3} = {x^3} + 9{x^2} + 27x + 27\)
5. Lập phương của một hiệu
\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
Ví dụ: \({\left( {x - 3} \right)^3} = {x^3} - 3{x^2}.3 + 3x{.3^2} - {3^3} = {x^3} - 9{x^2} + 27x - 27\)
6. Tổng hai lập phương
\({A^3} + {B^3} = (A + B)\left( {{A^2} - AB + {B^2}} \right)\)
Ví dụ: \({x^3} + 8 = {x^3} + {2^3} = (x + 2)({x^2} - 2x + 4)\)
7. Hiệu hai lập phương
\({A^3} - {B^3} = (A - B)\left( {{A^2} + AB + {B^2}} \right)\)
Ví dụ: \({x^3} - 8 = \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)\)
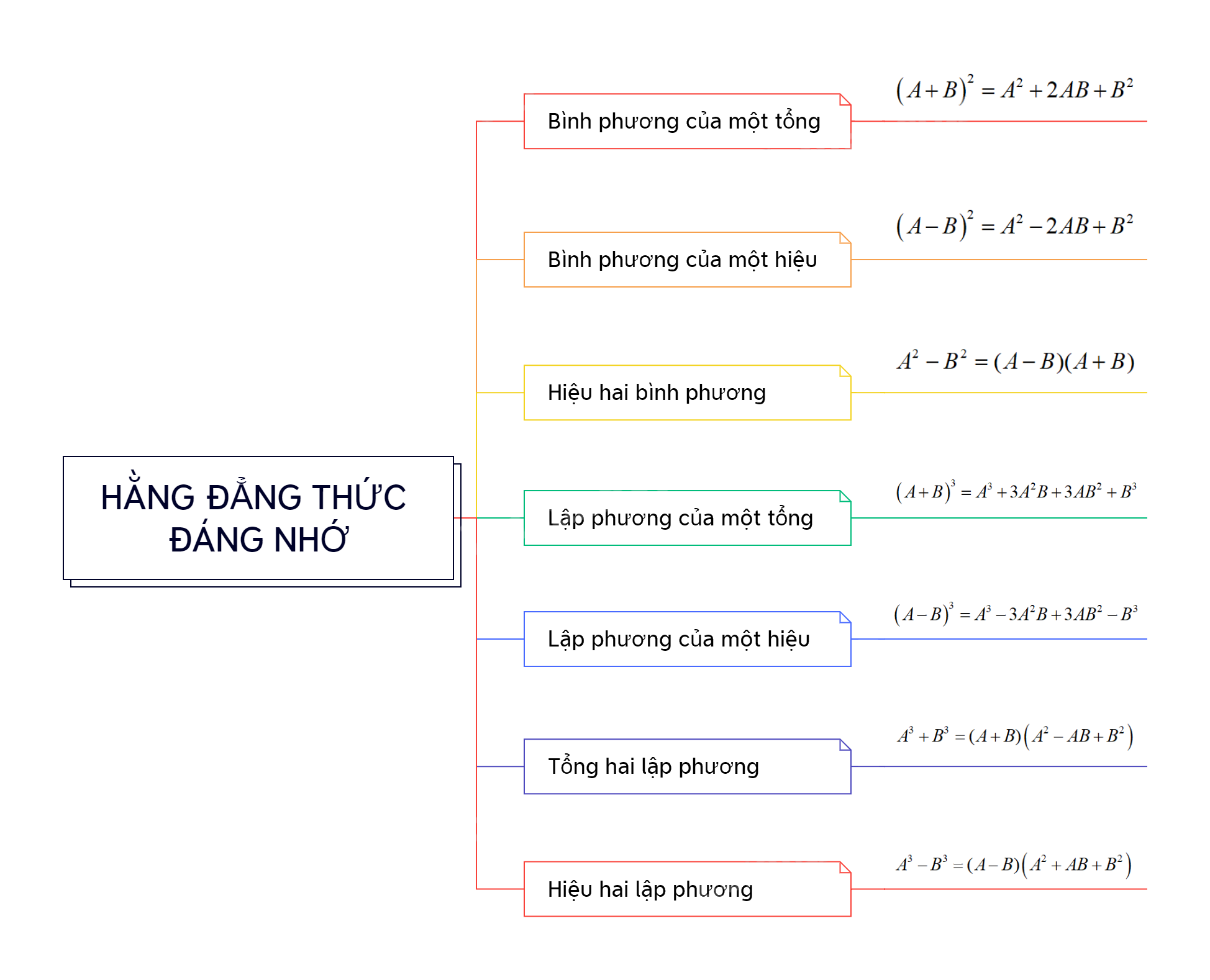
Hằng đẳng thức đáng nhớ là những biểu thức đại số luôn đúng với mọi giá trị của biến. Việc nắm vững các hằng đẳng thức này là chìa khóa để giải quyết nhiều bài toán đại số, đặc biệt là các bài toán liên quan đến phân tích đa thức thành nhân tử, rút gọn biểu thức và giải phương trình.
Các hằng đẳng thức trên có thể được chứng minh bằng cách khai triển trực tiếp hoặc sử dụng các phương pháp đại số khác. Ví dụ, để chứng minh hằng đẳng thức (a + b)² = a² + 2ab + b², ta có thể khai triển biểu thức (a + b)² như sau:
(a + b)² = (a + b)(a + b) = a(a + b) + b(a + b) = a² + ab + ba + b² = a² + 2ab + b²
Các hằng đẳng thức đáng nhớ có rất nhiều ứng dụng trong việc giải toán. Dưới đây là một số ví dụ:
Ví dụ 1: Phân tích đa thức x² - 9 thành nhân tử.
Ta có: x² - 9 = x² - 3² = (x + 3)(x - 3)
Ví dụ 2: Rút gọn biểu thức (2x + 1)² - (x - 1)²
Ta có: (2x + 1)² - (x - 1)² = (2x + 1 + x - 1)(2x + 1 - x + 1) = (3x)(x + 2) = 3x² + 6x
Hãy tự giải các bài tập sau để củng cố kiến thức về hằng đẳng thức đáng nhớ:
Khi sử dụng các hằng đẳng thức đáng nhớ, cần chú ý đến dấu của các số hạng và thứ tự của các biến. Việc nhầm lẫn về dấu hoặc thứ tự có thể dẫn đến kết quả sai.
Lý thuyết Hằng đẳng thức đáng nhớ là một phần quan trọng của chương trình Toán 8. Việc nắm vững các hằng đẳng thức này sẽ giúp bạn tự tin hơn trong việc giải các bài toán đại số. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.