Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 8 trang 72 SGK Toán 8 tập 2 – Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và phù hợp với chương trình học Toán 8 hiện hành. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
a) Trong Hình 20a, cho biết
Đề bài
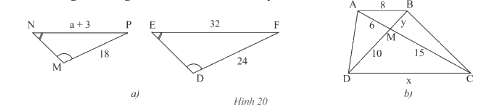
a) Trong Hình 20a, cho biết \(\widehat N = \widehat E,\widehat M = \widehat D,MP = 18m,DF = 24m,\)\(EF = 32m,\)\(NP = a + 3\left( m \right)\). Tìm \(a\).
b) Cho \(ABCD\) là hình thang \(\left( {AB//CD} \right)\) (Hình 20b).
Chứng minh rằng \(\Delta AMB\backsim\Delta CMD\). Tìm \(x,y\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau.
- Hai tam giác đồng dạng thì các cặp cạnh tương ứng có cùng tỉ lệ.
Lời giải chi tiết
a) Xét tam giác \(MNP\) tam giác \(DEF\) ta có:
\(\widehat M = \widehat D\) (giả thuyết)
\(\widehat N = \widehat E\) (giả thuyết)
Do đó, \(\Delta MNP\backsim\Delta DEF\) (g.g)
Suy ra, \(\frac{{MP}}{{DF}} = \frac{{NP}}{{EF}} \Rightarrow \frac{{18}}{{24}} = \frac{{a + 3}}{{32}} \Rightarrow a + 3 = \frac{{18.32}}{{24}} = 24 \Leftrightarrow a = 24 - 3 = 21\).
Vậy \(a = 21m\).
b) Vì \(ABCD\) là hình thang nên \(AB//CD\).
Vì \(AB//CD \Rightarrow \widehat {ABM} = \widehat {MDC}\) (hai góc so le trong) và \(AB//CD \Rightarrow \widehat {BAM} = \widehat {MCD}\) (hai góc so le trong)
Xét tam giác \(AMB\) và tam giác \(CMD\) có:
\(\widehat {ABM} = \widehat {MDC}\) (chứng minh trên)
\(\widehat {BAM} = \widehat {MCD}\) (chứng minh trên)
Do đó, \(\Delta AMB\backsim\Delta CMD\) (g.g).
Ta có:
\(\frac{{AM}}{{CM}} = \frac{{BM}}{{DM}} = \frac{{AB}}{{CD}} \Leftrightarrow \frac{6}{{15}} = \frac{y}{{10}} = \frac{8}{x}\).
Ta có: \(\frac{6}{{15}} = \frac{y}{{10}} \Rightarrow y = \frac{{10.6}}{{15}} = 4\)
\(\frac{6}{{15}} = \frac{8}{x} \Rightarrow x = \frac{{8.15}}{6} = 20\).
Vậy \(x = 20;y = 4\).
Bài 8 trang 72 SGK Toán 8 tập 2 – Chân trời sáng tạo thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về tính chất của hình thang cân để giải quyết các bài toán liên quan đến việc chứng minh, tính toán độ dài cạnh, góc và đường trung bình của hình thang cân.
Bài 8 trang 72 SGK Toán 8 tập 2 – Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giải bài 8 trang 72 SGK Toán 8 tập 2 – Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Bài toán: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài đường cao của hình thang.
Giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là đường cao của hình thang.
Vì ABCD là hình thang cân nên DH = KC = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.
Áp dụng định lý Pitago vào tam giác ADH vuông tại H, ta có:
AH2 = AD2 - DH2 = 62 - 2.52 = 36 - 6.25 = 29.75
Suy ra, AH = √29.75 ≈ 5.45cm.
Vậy, đường cao của hình thang ABCD là khoảng 5.45cm.
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và sách bài tập Toán 8 tập 2 – Chân trời sáng tạo. Ngoài ra, có thể tham khảo các bài giảng trực tuyến và các nguồn tài liệu học tập khác.
Kiến thức về hình thang cân là nền tảng quan trọng cho việc học các chương trình Toán học ở các lớp trên. Việc nắm vững các tính chất và phương pháp giải bài tập về hình thang cân sẽ giúp học sinh tự tin hơn trong việc giải quyết các bài toán hình học phức tạp.
Bài 8 trang 72 SGK Toán 8 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình thang cân và các ứng dụng của nó. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, học sinh sẽ tự tin hơn trong việc giải quyết bài tập này và đạt kết quả tốt trong môn Toán.